EiMedBiom - Blatt 6

Aufgabe 1

In der Kardiologie wurde eine Kohortenstudie ($n=931$) durchgeführt, in der das Auftreten einer milden unerwünschten Arzneimittelwirkung (UAW) in Abhängigkeit von folgenden potenziellen Risikofaktoren untersucht werden sollte:

Variable	Beschreibung
Statin	Statin verordnet / Statin nicht verordnet
Alter	in Jahren
Geschlecht	weiblich / männlich
Hämatokrit	in g/dl

Die Referenzkategorie ist jeweils unterstrichen.

Für die Auswertung wurde ein logistisches Regressionsmodell angewendet. Im Folgenden sehen Sie einen Teil des R-Outputs für das Endmodell (${\beta }^T=(\alpha ,{\beta }_1,{\beta }_2,{\beta }_3,{\beta }_4{)}^T$):

Coefficients:

Coefficient	Estimate	Std. Error
(Intercept)	-1.75544	0.78492
Statin	0.14692	0.26833
Geschlecht	0.37668	0.18705
Alter	0.03694	0.01383
Statin:Geschlecht	1.12018	0.34857

(a) In diesem Datensatz gibt es 33 Frauen, die 54 Jahre alt sind und denen Statin verordnet wurde. Bei wie vielen dieser Frauen erwarten Sie eine UAW?

Logistische Regressionsmodelle und Log-Odds nicht verstanden? → Logistische Regression Odds vs. Wahrscheinlichkeit

Um die erwartete Anzahl der Frauen mit UAW zu berechnen, verwenden wir das logistische Regressionsmodell:

1. Log-Odds berechnen:

   $$\text{log(odds)}={\beta }_0+{\beta }_1\cdot \text{Statin}+{\beta }_2\cdot \text{Geschlecht}+{\beta }_3\cdot \text{Alter}+{\beta }_4\cdot (\text{Statin}\times \text{Geschlecht})$$

   Einsetzen der Koeffizienten und Werte (Statin = 1, Geschlecht = 1 (weiblich), Alter = 54):

   $$\text{log(odds)}=-1.75544+0.14692\cdot 1+0.37668\cdot 1+0.03694\cdot 54+1.12018\cdot (1\cdot 1)$$ $$=-1.75544+0.14692+0.37668+1.99476+1.12018=1.8831$$

2. Odds in Wahrscheinlichkeit umrechnen:

   $$\text{Odds}=e^{1.8831}\approx 6.576\Rightarrow p=\frac{6.576}{1+6.576}\approx 0.868(86.8\%)$$

3. Erwartete Anzahl:

   $$33\cdot 0.868\approx \lfloor 28.64\rfloor \approx 28$$

Antwort: Bei etwa 28 der 33 Frauen erwarten wir eine UAW.

(b) Berechnen Sie das Odds Ratio der unter (a) definierten Patientengruppe im Vergleich zu Männern, die kein Statin verordnet bekamen und 73 Jahre alt sind.

$$\text{log(odds)}={\beta }_0+{\beta }_1\cdot \text{Statin}+{\beta }_2\cdot \text{Geschlecht}+{\beta }_3\cdot \text{Alter}+{\beta }_4\cdot (\text{Statin}\times \text{Geschlecht})$$

Einsetzen

$$\text{log(odds)}=-1.75544+0.14692\cdot 0+0.37668\cdot 0+0.03694\cdot 73+1.12018\cdot (0\cdot 0)$$ $$=0.94118$$

Log-Odds beider Gruppen

Wichtig

$$OR=e^{\Delta \log (\text{odds})}$$

Du hast kein Plan warum wir diese Formel brauchen? → Erklärung Warum wir die Differenz der Log-Odds verwenden und nicht die Division

1. Frauen mit Statin (54. Jahre) $$\log ({\text{Odds}}_{\text{Frauen}})=1.8831$$
2. Männer ohne Statin (73 Jahre)

$$\log ({\text{Odds}}_{\text{Ma¨nner}})=0.94118$$

Differenz dieser log Odds

Tipp

Du hast kein Plan warum wir hier subtrahieren und nicht dividieren? → Erklärung Warum wir die Differenz der Log-Odds verwenden und nicht die Division

$$\begin{array}{rl}\Delta \log (\text{odds})& =\log ({\text{Odds}}_{\text{Frauen}})-\log ({\text{Odds}}_{\text{Ma¨nner}})\\ & =1.8831-0.94118\\ & =0.94192\end{array}$$

Damit nun Odds berechnen

$$\begin{array}{rl}OR& =e^{\Delta \log (\text{odds})}\\ & =e^{0.94192}\\ & =2.5649\end{array}$$

→ Die OR dafür, dass eine Frau mit Statin im Alter von 54 Jahren eine UAW hat ist ungefähr 2.56 mal größer als ein Mann ohne Statin im Alter von 73 Jahren

(c) Überprüfen Sie anhand eines geeigneten Tests, ob der Effekt von Alter statistisch signifikant ist. Berechnen Sie analog für den Regressionskoeffizienten von Alter ein 95%-Wald-Konfidenzintervall.

Wald-Test – Kurz & Knackig

Zweck: Prüft, ob ein Regressionskoeffizient (z. B. für Alter) signifikant von Null abweicht.

Formel & Schritte

1. Teststatistik berechnen: $$z=\frac{\hat{\beta }}{\text{SE}(\hat{\beta })}\text{(Koeffizient ÷ Standardfehler)}$$
2. Entscheidung:
   • Kritischer Wert bei $\alpha =0.05$: $z_{0.975}=1.96$.
   • $|z|>1.96$ → Signifikanter Effekt ($p<0.05$).

Beispiel – Alter in der Studie

• ${\hat{\beta }}_3=0.03694$, $\text{SE}=0.01383$.
• Teststatistik: $$z=\frac{0.03694}{0.01383}\approx 2.67(2.67>1.96\to \ast \ast signifikant!\ast \ast )$$

95%-Wald-Konfidenzintervall

• Formel: $$\hat{\beta }\pm 1.96\cdot \text{SE}(\hat{\beta })$$
• Berechnung: $$0.03694\pm 1.96\cdot 0.01383\to [0.0098;0.0640]$$
• Interpretation:
  • Intervall enthält nicht die Null → Alter ist signifikant.
  • Effektstärke: Pro Lebensjahr steigen die Log-Odds für UAW um 0.0098 bis 0.0640.

Warum Wald-Test?

• Vorteile:
  • Schnell: Nutzt direkt $\hat{\beta }$ und $\text{SE}$ aus der Regression.
  • Keine zusätzlichen Modellrechnungen nötig (z. B. beim LRT).
• Nachteil: Bei kleinen Stichproben ($n<100$) ungenau → besser LRT.

Typische Fragen

Frage: “Warum steht im Output ein $z$-Wert und kein $t$-Wert?”
Antwort: In der logistischen Regression wird asymptotische Normalverteilung angenommen (große $n$) → $z$-Werte.

Frage: “Was, wenn das KI die Null einschließt?”
Antwort: Dann ist der Effekt nicht signifikant (z. B. KI $[-0.1;0.2]$).

Zusammenfassung

• Wald-Test = Der Schnellcheck für Signifikanz in Regressionen.
• Merksatz:
  “Z-Wert über 1.96 – der Effekt ist nicht von Null!” 😉

1. Überprüfung der statistischen Signifikanz des Alterseffekts

a) Wahl des Tests:
Um zu prüfen, ob der Effekt des Alters signifikant ist, verwenden wir den Wald-Test.
Warum?

• Der Wald-Test nutzt direkt den geschätzten Koeffizienten (${\hat{\beta }}_3=0.03694$) und seinen Standardfehler ($\text{SE}=0.01383$) aus dem Regressionsoutput.
• Er ist einfach durchzuführen, da keine zusätzlichen Modellrechnungen (z. B. Likelihood-Ratio-Test) erforderlich sind.
• Bei großen Stichproben ($n=931$) ist der Wald-Test zuverlässig.

b) Berechnung der Teststatistik:

$$z=\frac{{\hat{\beta }}_3}{\text{SE}({\hat{\beta }}_3)}=\frac{0.03694}{0.01383}\approx 2.67$$

c) Entscheidung:

• Kritischer Wert bei $\alpha =0.05$ (zweiseitig): $z_{0.975}=1.96$.
• Da $|z|=2.67>1.96$, lehnen wir die Nullhypothese ab.
• Ergebnis: Der Effekt des Alters ist statistisch signifikant ($p<0.05$).

2. Berechnung des 95%-Wald-Konfidenzintervalls für ${\beta }_3$ (Alter)

a) Formel:

$${\hat{\beta }}_3\pm 1.96\cdot \text{SE}({\hat{\beta }}_3)$$

b) Berechnung:

$$\begin{array}{rl}\text{Untere Grenze}& =0.03694-1.96\cdot 0.01383\approx 0.0098,\\ \text{Obere Grenze}& =0.03694+1.96\cdot 0.01383\approx \mathrm{0.0640.}\end{array}$$

c) Interpretation:

• Das 95%-Konfidenzintervall für ${\beta }_3$ ist $[0.0098;0.0640]$.
• Da die Null nicht im Intervall liegt, bestätigt dies die Signifikanz des Alterseffekts.
• Effektstärke: Pro zusätzlichem Lebensjahr steigen die Log-Odds für eine UAW um 0.0098 bis 0.0640.
• Odds Ratio: $e^{0.0098}\approx 1.01$ bis $e^{0.0640}\approx 1.07$.

3. Fazit

• Alter hat einen signifikant positiven Einfluss auf das Auftreten einer UAW ($p<0.05$).
• 95%-Konfidenzintervall: $[0.0098;0.0640]$.
• Praxisrelevanz: Obwohl der Effekt klein ist, ist er statistisch nachweisbar.

(d) Ein Kollege berechnet ein weiteres logistisches Regressionsmodell, indem er zusätzlich den potenziellen Einflussfaktor Hämatokrit berücksichtigt. Der entsprechende R-Output für das Endmodell lautet:

Coefficients:

Coefficient	Estimate	Std. Error
(Intercept)	1.84289	0.79758
Statin	-0.14232	0.26846
Geschlecht	-0.37883	0.18714
Alter	-0.03702	0.01384
Hämatokrit	-0.16562	0.25825
Statin:Geschlecht	-1.12703	0.34881

Was fällt Ihnen auf? Können Sie dieses Ergebnis „reparieren“?

Multikollinearität – Kurz erklärt

Was ist das?
Multikollinearität liegt vor, wenn zwei oder mehr Prädiktoren in einem Regressionsmodell stark korreliert sind. Das führt dazu, dass die Schätzung der Koeffizienten instabil wird (z. B. Vorzeichenumkehr) und schwer interpretierbar ist.

Warum ist das ein Problem?

• Die Effekte der korrelierten Variablen lassen sich nicht mehr eindeutig trennen.
• Standardfehler der Koeffizienten werden aufgebläht → Signifikanztests unzuverlässig.

Wie erkennt man es?

1. Variance Inflation Factor (VIF):
   • VIF > 5: Moderate Multikollinearität.
   • VIF > 10: Schwere Multikollinearität.
2. Korrelationsmatrix: Prüfe, ob Prädiktorenpaare Korrelationen > |0.7| haben.

Beispiel aus der Aufgabe (d):
Nach Hinzufügen von Hämatokrit kehren sich die Vorzeichen anderer Koeffizienten um. Mögliche Ursache: Hämatokrit ist stark mit Alter oder Geschlecht korreliert.

Lösungen:

• Variablen entfernen: Den am wenigsten theoriefundierten Prädiktor streichen.
• Daten kombinieren: Aus stark korrelierten Variablen einen Index bilden (z. B. PCA).
• Mehr Daten sammeln: Reduziert zufällige Korrelationen.

Typische Fragen
”Warum nicht einfach Korrelationen prüfen?”
→ Die VIF berücksichtigt alle Prädiktoren gleichzeitig, nicht nur paarweise Korrelationen.

”Was tun, wenn ich Variablen nicht entfernen darf?”
→ Ridge-Regression verwenden, die Multikollinearität stabilisiert.

Merksatz:
“VIF über 5? 🚩 – Zeit zum Handeln!” 😉

Auffälligkeiten

1. Vorzeichenumkehr:
   Die Koeffizienten für Statin, Geschlecht, Alter und Statin:Geschlecht haben im Vergleich zum ursprünglichen Modell gegenläufige Vorzeichen (z. B. Statin: von +0.14692 auf -0.14232). Dies deutet auf Multikollinearität oder eine fehlende Interaktion hin.

2. Fehlende Interaktion:
   Es gibt einen Interaktionsterm Statin:Geschlecht, aber keinen Term Hämatokrit:Geschlecht. Falls der Effekt von Hämatokrit geschlechtsspezifisch ist, verzerrt dies die Schätzungen.

Reparatur-Schritte

1. Interaktion hinzufügen:
   Erweitere das Modell um Hämatokrit:Geschlecht:

   formula = UAW ~ Statin + Geschlecht + Alter + Hämatokrit + Statin:Geschlecht + Hämatokrit:Geschlecht

   Begründung: Der Effekt von Hämatokrit könnte bei Frauen und Männern unterschiedlich sein.

2. Multikollinearität prüfen:
   Berechne die Variance Inflation Factors (VIF) für alle Prädiktoren:

   • VIF > 5 → Prädiktor entfernen/kombinieren.
   • Verdacht: Hämatokrit könnte mit Alter/Geschlecht korrelieren.

3. Modell neu anpassen:
   Nach Hinzufügen der Interaktion prüfen, ob sich die Vorzeichen stabilisieren.

Ergebnis

• Durch Hämatokrit:Geschlecht werden geschlechtsspezifische Effekte abgebildet.
• Die Vorzeichenumkehr der anderen Koeffizienten verschwindet wahrscheinlich.

Antwort:
Das Modell lässt sich reparieren, indem man Hämatokrit:Geschlecht hinzufügt und Multikollinearität prüft.

(e) Die Devianz des Regressionsmodells aus Aufgabe (a) beträgt 1028,437, die Devianz des Regressionsmodells aus Aufgabe (d) beträgt 1028,849. Führen Sie einen Likelihood-Quotienten-Test (LRT) durch und interpretieren Sie das Ergebnis.

Hinweis: Die Devianz ist definiert für ein Modell $M_k$ als $D=-2\log \left(\frac{L({\hat{\beta }}_{M_k})}{L({\hat{\beta }}_{\text{max}})}\right)$, wobei $L({\hat{\beta }}_{\text{max}})$ die Likelihood des saturierten Modells ist (nicht angegeben).

Schritte des Likelihood-Quotienten-Tests (LRT)

1. Nullhypothese ($H_0$): Das komplexere Modell (d) mit Hämatokrit bietet keinen signifikanten Vorteil gegenüber dem einfacheren Modell (a).

2. Teststatistik:

   $$\text{LRT}=D_{\text{einfach}}-D_{\text{komplex}}=1028.437-1028.849=-0.412$$

   Hinweis: Ein negativer Wert bedeutet, dass das komplexe Modell eine schlechtere Anpassung hat als das einfache Modell.

3. Entscheidung:

   • Die Teststatistik folgt einer ${\chi }^2$-Verteilung mit $df=1$ (weil Modell (d) 1 zusätzlichen Parameter enthält).
   • Kritischer Wert bei $\alpha =0.05$: ${\chi }_{0.95}^2(1)=3.841$.
   • Da $-0.412<3.841$, kann $H_0$ nicht verworfen werden.

Interpretation

• Ergebnis: Das Hinzufügen von Hämatokrit verbessert das Modell nicht signifikant ($p>0.05$).
• Praktische Bedeutung: Hämatokrit trägt in diesem Kontext nicht zur Erklärung der UAW bei.
• Achtung: Der negative LRT-Wert deutet darauf hin, dass das komplexe Modell sogar schlechter passt als das einfache Modell – ein klares Zeichen, dass Hämatokrit keinen Nutzen hat.

---

Aufgabe 2

In einer Studie mit $n=502$ Personen wurde der Zusammenhang zwischen der Lebenszufriedenheit einer Person und der Anzahl $x$ ihrer positiven Tagesereignisse in den letzten 24 Stunden untersucht. Personen markierten auf einer Liste von 30 positiven Tagesereignissen alle, die sie in den letzten 24 Stunden erlebt hatten. Die abhängige Variable Lebenszufriedenheit wurde anhand des Items „Ich bin mit meinem Leben zufrieden“ erfasst. Der Antwort „ja“ wurde der Wert 1, der Antwort „nein“ der Wert 0 zugeordnet. Eine Analyse des Zusammenhangs beider Variablen auf Basis einer logistischen Regression mit Prädiktor $\eta ={\beta }_0+{\beta }_{1}x$ ergab folgende Ergebnisse: ${\beta }_0=0.0113$ und ${\beta }_1=0.0728$.

(a) Stellen Sie das zugehörige Regressionsmodell auf und interpretieren Sie die Parameter ${\beta }_0$ und ${\beta }_1$.

Unzureichende Lösung

$$\log (\text{Odds})=0.0113+0.0728\cdot x$$

• ${\beta }_0=0.0113$ steht für die Grundlebenszufriedenheit, die eine Person hat, unabhängig von der Anzahl $x$ ihrer positiven Tagesereignisse
• ${\beta }_1=0.0728$ steht für die zusätzliche Lebenszufriedenheit, die pro Anzahl $x$ der positiven Tagesereignisse der Personen zur Grundlebenszufriedenheit addiert wird.

Regressionsmodell:

$$\log \left(\frac{P(\text{Ja})}{1-P(\text{Ja})}\right)={\beta }_0+{\beta }_{1}x=0.0113+0.0728\cdot x$$

Interpretation der Parameter:

1. ${\beta }_0=0.0113$:
   Dies ist der log-Odds der Lebenszufriedenheit, wenn eine Person keine positiven Tagesereignisse hatte ($x=0$).

   • Inhaltlich: Bei $x=0$ beträgt die Wahrscheinlichkeit für “Ja” etwa $\frac{e^{0.0113}}{1+e^{0.0113}}\approx 50.3\%$ (sehr knapp über 50%).
   • Formulierungen wie “Grundlebenszufriedenheit” sind intuitiv, sollten aber klar auf den log-Odds-Bezug hinweisen.

2. ${\beta }_1=0.0728$:
   Dieser Koeffizient gibt die Änderung der log-Odds der Lebenszufriedenheit pro zusätzlichem positiven Tagesereignis an.

   • Einfacher ausgedrückt: Mit jedem positiven Ereignis erhöhen sich die log-Odds um $0.0728$.
   • Odds-Ratio-Interpretation: Die Odds selbst vervielfachen sich pro Ereignis um $e^{0.0728}\approx 1.075$ (d. h., sie steigen um etwa $7.5\%$).

Kritik an meiner eigentlichen Lösung:

• Die Formulierung “zusätzliche Lebenszufriedenheit” ist irreführend, da es sich nicht um eine direkte Erhöhung der Lebenszufriedenheit (als metrische Variable), sondern um die log-Odds der binären Antwort handelt.
• Präzisieren Sie, dass ${\beta }_0$ und ${\beta }_1$ Effekte auf der Skala der logarithmierten Chancen abbilden.

Korrekte Kurzantwort:

• ${\beta }_0$: Log-Odds der Lebenszufriedenheit bei $x=0$.
• ${\beta }_1$: Erhöhung der log-Odds pro zusätzlichem positiven Ereignis.

(b) Wie ändern sich die Chancen für Lebenszufriedenheit, wenn die Anzahl an positiven Tagesereignissen um 10 ansteigt?

Lebenszufriedenheit mit 10 positiven Tagen

$$\begin{array}{rl}\log \left(\frac{P(\text{Ja})}{1-P(\text{Ja})}\right)& ={\beta }_0+{\beta }_{1}x\\ & =0.0113+0.0728\cdot x\\ & =0.0113+0.0728\cdot 10\\ & =0.7393\end{array}$$ $$e^{0.7393}=2.0945$$

Man sollte die Wahrscheinlichtkeit nicht berechnen nur die Chance (Odds)

$$\begin{array}{rl}\text{Chance}& =\frac{2.0945}{1+2.0945}\\ & =0.6768\\ & \approx 67.7\%\end{array}$$

Lebenszufriedenheit mit 0 positiven Tagen

$$\begin{array}{rl}\log \left(\frac{P(\text{Ja})}{1-P(\text{Ja})}\right)& ={\beta }_0+{\beta }_{1}x\\ & =0.0113+0.0728\cdot x\\ & =0.0113+0.0728\cdot 0\\ & =0.0113\end{array}$$

• Ergebnis: $$e^{0.0113}=1.0114$$

Man sollte die Wahrscheinlichtkeit nicht berechnen nur die Chance (Odds)

$$\begin{array}{rl}\text{Chance}& =\frac{1.0114}{1+1.0114}\\ & =0.5028\\ & \approx 50.3\%\end{array}$$

Antwort

Man sollte die Wahrscheinlichtkeit nicht berechnen nur die Chance (Odds)

→ Die Lebenszufriedenheit steigt um $17.4\%$ $(67.7\%-50.3\%)$

$$\text{Odds}=\frac{2.0945}{1.0114}=2.07$$

→ Die Chancen für Lebenszufriedenheit verdoppeln sich (Odds-Ratio ≈ 2.07), wenn die Anzahl positiver Tagesereignisse um 10 steigt.

(c) Berechnen Sie die Wahrscheinlichkeit, mit dem Leben zufrieden zu sein, für eine Person, die 10 positive Tagesereignisse angegeben hat.

$$\begin{array}{rl}\log \left(\frac{P(\text{Ja})}{1-P(\text{Ja})}\right)& ={\beta }_0+{\beta }_{1}x\\ & =0.0113+0.0728\cdot x\\ & =0.0113+0.0728\cdot 10\\ & =0.7393\end{array}$$ $$e^{0.7393}=2.0945$$ $$\begin{array}{rl}\text{P(Zufrieden mit dem Leben)}& =\frac{2.0945}{1+2.0945}\\ & =0.6768\\ & \approx 67.7\%\end{array}$$

→ Eine Person die 10 positive Tagesereignisse angegeben hat, hat eine $67.7\%$ Wahrscheinlichkeit zufrieden mit dem Leben zu sein

(d) Plotten Sie in $R$ die Wahrscheinlichkeit, mit dem Leben zufrieden zu sein, in Abhängigkeit von der Anzahl an positiven Tagesereignissen.

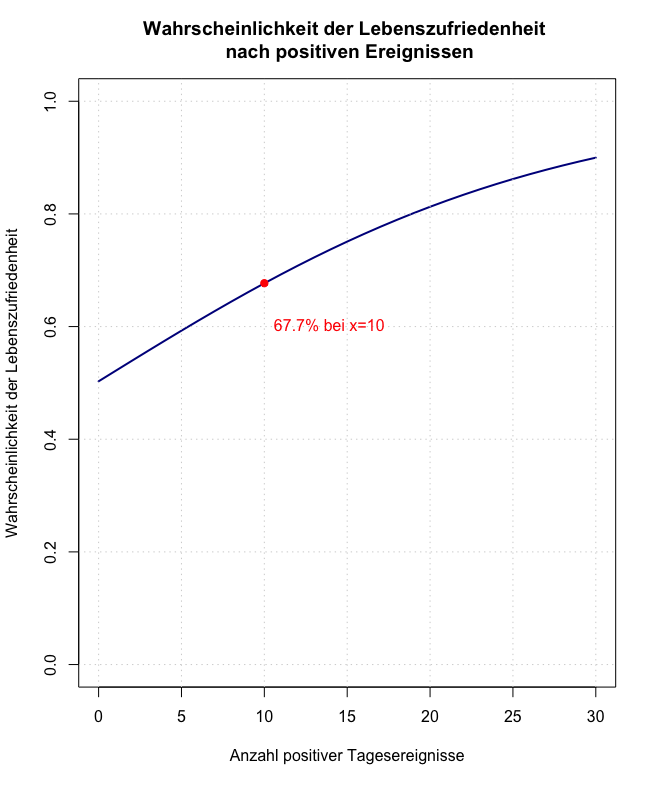
# Koeffizienten aus der logistischen Regression
beta0 <- 0.0113
beta1 <- 0.0728
 
# Bereich der positiven Tagesereignisse (0 bis 30, da 30 die maximale Anzahl ist)
x <- seq(0, 30, by = 1)
 
# Berechnung der Wahrscheinlichkeiten P(Y=1)
log_odds <- beta0 + beta1 * x
prob <- exp(log_odds) / (1 + exp(log_odds))  # Alternativ: plogis(log_odds)
 
# Plot erstellen
plot(x, prob,
     type = "l",        # Linienplot
     col = "darkblue",
     lwd = 2,
     xlab = "Anzahl positiver Tagesereignisse",
     ylab = "Wahrscheinlichkeit der Lebenszufriedenheit",
     main = "Wahrscheinlichkeit der Lebenszufriedenheit nach positiven Ereignissen",
     ylim = c(0, 1))    # Y-Achse von 0 bis 1
 
# Raster hinzufügen
grid()
 
# Hervorhebung des Beispiels aus Teil (c): x = 10
points(10, 0.677, col = "red", pch = 19)
text(10, 0.6, "67.7% bei x=10", col = "red", pos = 4)

---

×

MyUniNotes is a free, non-profit project to make education accessible for everyone. If it has helped you, consider giving back! Even a small donation makes a difference.

These are my personal notes. While I strive for accuracy, I’m still a student myself. Thanks for being part of this journey!