Aufgabe 1
In einer Studie von Woodward und Walker (1994) wurde der Zusammenhang zwischen Zuckerkonsum und Karies in 61 Entwicklungsländern und 29 Industrieländern untersucht. Der Datensatz
sugar.consumption.txtenthält den Konsum von Zucker (in kg/Person/Jahr) gemittelt über 5 Jahre (sugar), die durchschnittliche Anzahl verfaulter / fehlender Zähne oder Zähne mit Füllung (dmft) und einen Indikator ob es sich um ein Industrie- oder Entwicklungsland handelt (industrialized).
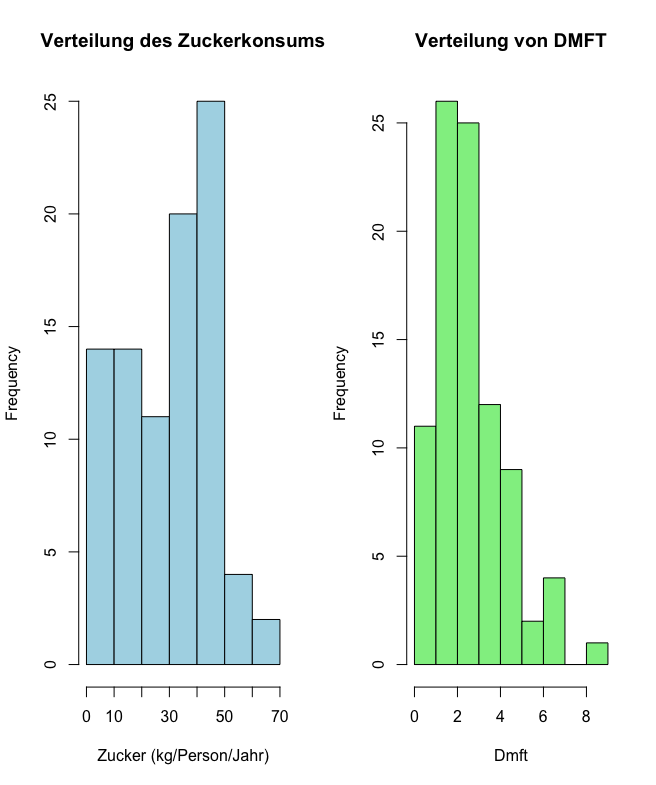
(a) Lesen Sie die Daten in R mittels des Befehls read.table() ein. Stellen Sie jeweils die Verteilung für sugar und für dmft in einem geeigneten Plot dar.
data <- read.table("data/sugar_consumption.txt", header = TRUE)
head(data)
hist(data$sugar, main = "Verteilung des Zuckerkonsums", xlab = "Zucker (kg/Person/Jahr)")
hist(data$dmft, main = "Verteilung von DMFT", xlab = "Durchschnittliche Anzahl verfaulter/fehlender Zähne")
Erklärung warum hier
plotnicht passtEin einfacher
plotwieplot(data$sugar, data$dmft)erstellt ein Streudiagramm (Scatterplot), das den Zusammenhang zwischensugarunddmftzeigt. Die Aufgabenstellung verlangt jedoch, die Verteilung jeder Variable einzeln darzustellen. Dafür sind Histogramme oder ähnliche Diagramme besser geeignet, da sie die Häufigkeit oder Spannweite der Werte einer einzelnen Variable visualisieren.
Output:
(b) Erstellen Sie ein Streudiagramm für die Variablen sugar (x-Achse) und dmft (y-Achse). (Tipp: R-Befehl plot().)
plot(data$sugar,data$dmft,main = "Zusammenhang zwischen Zucker und DMFT",xlab = "Sugar", ylab="dmft", col="red",pch=20)Output:

(c) Berechnen Sie den Korrelationskoeffizienten nach Pearson zur Quantifizierung der Stärke des Zusammenhangs zwischen sugar und dmft unter Verwendung der Formel:
Besteht ein Zusammenhang zwischen Zuckerkonsum und Karies?
# Aufgabe 1c
correlation.one <- cor(data$sugar,data$dmft, method = c("pearson"))
correlation.test <- cor.test(data$sugar,data$dmft, method = c("pearson"))
print(correlation.test)Output:
Pearson\'s product-moment correlation
data: data$sugar and data$dmft
t = 5.0594, df = 88, p-value = 2.279e-06
alternative hypothesis: true correlation is not equal to 0
95 percent confidence interval:
0.2967797 0.6207627
sample estimates:
cor
0.4746958Antwort:
- Ja, es besteht ein signifikanter Zusammenhang zwischen Zuckerkonsum und Karies. Der Pearson-Korrelationskoeffizient von 0.4747 zeigt eine positive Korrelation mittlerer Stärke zwischen den Variablen
sugarunddmft. Der t-Wert von 5.0594 unterstützt die Ablehnung der Nullhypothese (), und der sehr kleine p-Wert von 2.279e-06 bestätigt dies. Daher kann die Nullhypothese (: Es besteht kein Zusammenhang zwischen Zuckerkonsum und Karies) sicher abgelehnt werden.
Extra (weil ich es machen wollte):
# Anhang 1c (mein Interesse)
ggplot(data,aes(x=data$sugar,y=data$dmft))+
geom_point()+
geom_smooth(method = "lm", se = TRUE, color = "blue") +
stat_cor(method="pearson")+
theme_minimal()+
labs(
title = "Zusammenhang zwischen Zucker und dmft",
x = "Zucker (g)",
y = "dmft-Wert"
)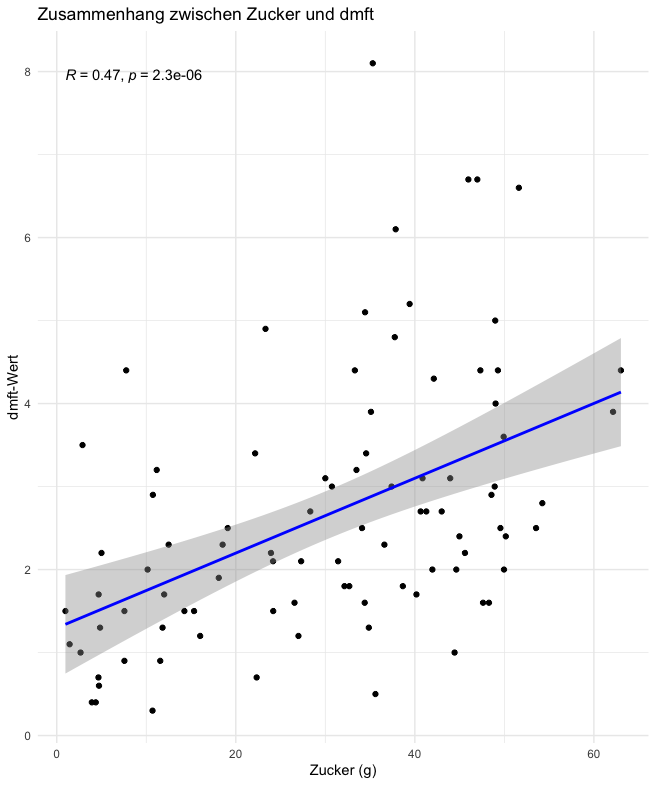
Was bedeuten die grauen Bereiche im Plot?
Die grauen Bereiche stellen das Konfidenzintervall für die Regressionslinie dar. Sie zeigen, wie sicher wir sind, dass die wahre Regressionslinie innerhalb dieses Bereichs liegt:
- Schmale Bereiche: Hohe Präzision der Schätzung, da die Punkte nahe an der Linie liegen.
- Breite Bereiche: Größere Unsicherheit, weil die Punkte stärker streuen.
Die Unsicherheit ist typischerweise an den Rändern der Daten größer, was zu breiteren grauen Bereichen führt.
(d) Berechnen Sie die Ränge für die Variablen sugar und dmft. Berechnen Sie den Korrelationskoeffizienten nach Spearman durch Ersetzen der -Werte und -Werte in der in (c) angegebenen Formel durch die von Ihnen berechneten Ränge. (Tipp: R-Befehl rank().)
Was sind Ränge und wie kann man sie verstehen?
Ränge beschreiben die Position eines Wertes innerhalb eines Datensatzes, nachdem alle Werte der Größe nach sortiert wurden. Der kleinste Wert bekommt Rang 1, der nächstgrößere Rang 2 usw. Bei gleichen Werten (Ties) teilen sich die Werte die Position und erhalten den Durchschnittsrang.
Formelle Beschreibung:
Sei ein geordneter Datensatz. Der Rang eines Wertes ist seine Position innerhalb des sortierten Datensatzes. Bei gleichen Werten wird der Rang als arithmetisches Mittel der betroffenen Positionen berechnet.Metapher zur Veranschaulichung:
Stell dir eine Gruppe von Schülern vor, die sich der Größe nach in einer Reihe aufstellen:
- Der kleinste Schüler steht an erster Stelle und bekommt Rang 1.
- Wenn zwei Schüler exakt gleich groß sind, teilen sie sich die Position und erhalten einen Durchschnittsrang (z. B. Rang 3.5, wenn sie auf den Positionen 3 und 4 stehen würden).
- Die Ränge geben also nicht die exakten Größen der Schüler wieder, sondern ihre relative Reihenfolge innerhalb der Gruppe.
Beispiel: Eine Liste von Zahlen:
10, 20, 15, 20.
- Der Wert
10(kleinster Wert) → Rang 1- Der Wert
15(nächstgrößerer Wert) → Rang 2- Die beiden Werte
20(gleich groß) → teilen sich die Ränge 3 und 4, also Durchschnittsrang 3.5.Wichtigkeit der Ränge:
Ränge sind besonders nützlich, um monotone Zusammenhänge zu untersuchen (z. B. mit der Spearman-Korrelation), da sie weniger empfindlich gegenüber Ausreißern sind. Im Gegensatz zu exakten Werten betrachten Ränge nur die Reihenfolge der Daten und ignorieren die Abstände zwischen den Werten.Frage eines Studierenden:
“Warum verwenden wir Ränge und nicht die Originalwerte bei der Spearman-Korrelation?”Antwort:
Die Spearman-Korrelation misst monotone Zusammenhänge, nicht notwendigerweise lineare. Die Originalwerte könnten durch Ausreißer verzerrt werden, was die Interpretation des Zusammenhangs erschwert. Ränge reduzieren diesen Effekt, da sie nur die relative Reihenfolge der Werte berücksichtigen und nicht deren exakte Abstände. Dadurch eignet sich die Spearman-Korrelation besser für nichtlineare oder gestörte Daten.
rank_sugar <- rank(data$sugar,na.last=TRUE)
rank_dmft<-rank(data$dmft,na.last=TRUE)
cor.test(rank_sugar,rank_dmft, method="spearman",data=data)Output:
Spearman\'s rank correlation rho
data: rank_sugar and rank_dmft
S = 58509, p-value = 1.664e-07
alternative hypothesis: true rho is not equal to 0
sample estimates:
rho
0.5183821Extra (weil ich es machen wollte):
# Anhang 1d (mein Interesse)
ggplot(data, aes(x = rank_sugar, y = rank_dmft)) +
geom_point() +
geom_smooth(method = "lm", se = TRUE, color = "blue") +
stat_cor(method = "spearman") +
theme_minimal() +
labs(
title = "Zusammenhang zwischen den Rängen von Zucker und dmft",
x = "Rang des Zuckerkonsums",
y = "Rang des dmft-Wertes"
)
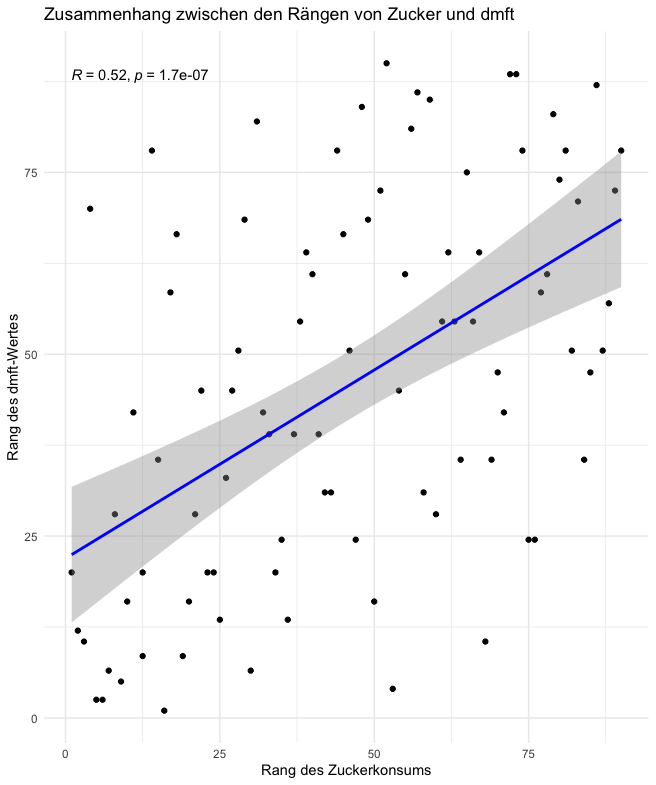
Was bedeuten die grauen Bereiche im Plot?
Die grauen Bereiche stellen das Konfidenzintervall für die Regressionslinie dar. Sie zeigen, wie sicher wir sind, dass die wahre Regressionslinie innerhalb dieses Bereichs liegt:
- Schmale Bereiche: Hohe Präzision der Schätzung, da die Punkte nahe an der Linie liegen.
- Breite Bereiche: Größere Unsicherheit, weil die Punkte stärker streuen.
Die Unsicherheit ist typischerweise an den Rändern der Daten größer, was zu breiteren grauen Bereichen führt.
(e) Erstellen Sie erneut ein Streudiagramm wie in Teilaufgabe (a). Verwenden Sie nun unterschiedliche Farben für Industrieländer und Entwicklungsländer. (Tipp: Argument col der Funktion plot().) Was fällt auf? Stützen Sie Ihre These durch Angabe geeigneter Maßeinheiten.
plot(
data$sugar, data$dmft,
main = "Zusammenhang zwischen Zucker und DMFT",
xlab = "Zucker (kg/Person/Jahr)",
ylab = "DMFT-Wert",
col = ifelse(data$industrialized == 1, "blue", "red"), # Farbe basierend auf 'industrialized'
pch = 20
)
legend("topright", legend = c("Industrieländer", "Entwicklungsländer"), col = c("blue", "red"), pch = 20)
Output
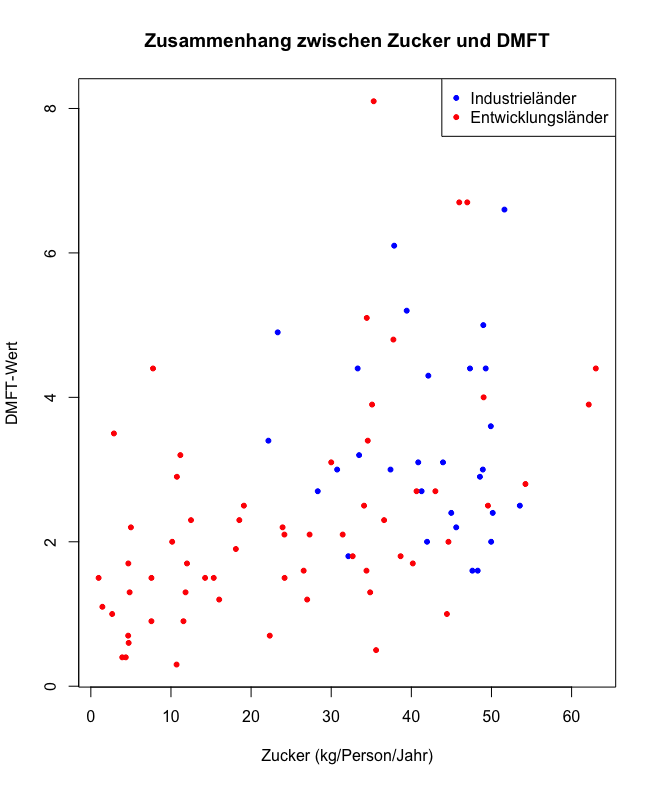
- Entwicklungsländer (rote Punkte)
- Geringer Zuckerkonsum (< 20 kg/Person/Jahr)
- Niedrige DMFT-Werte (0–3)
- Industrieländer (blaue Punkte)
- Höherer Zuckerkonsum (30–60 kg/Person/Jahr)
- Höhere DMFT-Werte (häufig 3–8)
- Interpretation:
- Höherer Zuckerkonsum → erhöhtes Kariesrisiko
- Industrieländer: bessere zahnmedizinische Versorgung, aber mehr Softdrinks & Süßigkeiten
- Entwicklungsländer: geringerer Zuckerkonsum, aber schlechtere Zahnpflege → unbehandelte Schäden
- Weitere Einflussfaktoren: Gesundheitsbildung, Fluoridversorgung, zahnmedizinische Infrastruktur
Aufgabe 2
Der Datensatz
Messungen.csventhält simulierte Messwerte für Individuen. Für jedes Individuum gibt es zwei Messungen, wobei eine Messung mittels eines Messverfahrens A und die andere Messung mittels eines Verfahrens B durchgeführt wurde.
(a) Lesen Sie die Daten in R ein und machen Sie sich einen Überblick über die Daten. Hinweis: Verwenden Sie den Befehl read.csv2() um die Daten einzulesen.
data <- read.csv2("data/Messungen.csv")
head(data)(b) Erstellen Sie ein Streudiagramm mit den Messwerten des Verfahrens A auf der x-Achse und den Messwerten des Verfahrens B auf der y-Achse. Zeichnen Sie die Gerade ein, auf der die Wertepaare bei perfekter Übereinstimmung der beiden Messmethoden liegen. (Tipp: R-Befehle plot() und abline().) Was fällt auf?
# Aufgabe 2b
# Extrahieren der Messwerte für die Verfahren A und B
method_A <- data$y[data$method == "A"]
method_B <- data$y[data$method == "B"]
# Erstellen eines Streudiagramms
plot(
method_A, method_B,
xlab = "Messwerte Verfahren A",
ylab = "Messwerte Verfahren B",
main = "Streudiagramm der Messwerte",
pch = 16,
col = "blue"
)
abline(0, 1, col = "red", lwd = 2)Output:
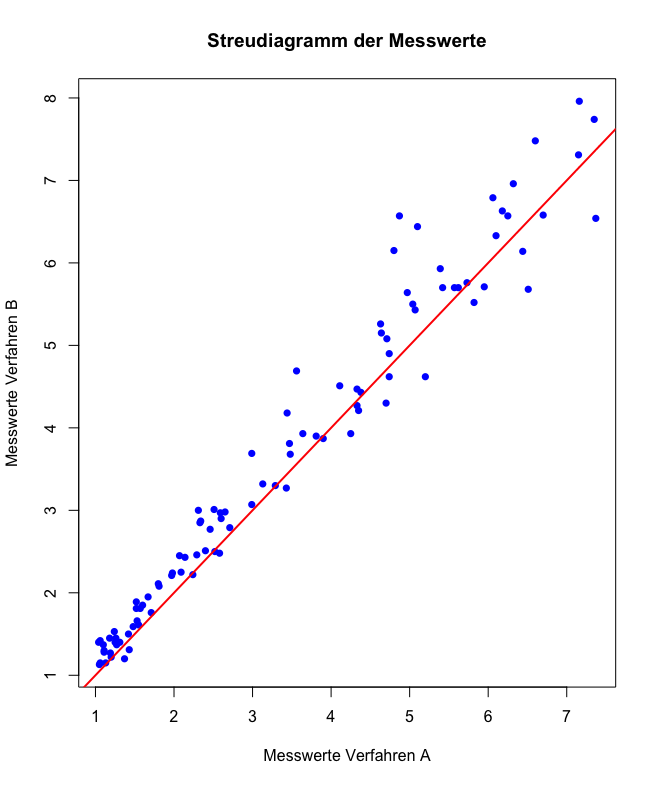
Antwort:
- Die Wertepaare liegen bei kleinen Werten sehr nahe an der Geraden , was auf eine hohe Übereinstimmung der Messmethoden hinweist. Bei größeren Werten werden die Abweichungen jedoch zunehmend größer, was auf eine geringere Genauigkeit der Methode bei höheren Messwerten schließen lässt.
Extra (Mit Differenzierung):
# Erstellen eines Streudiagramms
plot(
method_A, method_B,
xlab = "Messwerte Verfahren A",
ylab = "Messwerte Verfahren B",
main = "Streudiagramm der Messwerte",
pch = 16,
col = ifelse(data$method == "A", "red", "blue"), # Farbe basierend auf 'industrialized'
)
abline(0, 1, col = "orange", lwd = 2)+
legend("topleft", legend = c("Methode = A", "Methode = B"), col = c("red", "blue"), pch = 20)
(c) Erstellen Sie einen Bland-Altman Plot (Tipp: R-Befehle plot() und abline()). Interpretieren Sie das Ergebnis. Welche Probleme treten bei der Interpretation auf?
Was ist ein Bland-Altman-Plot und wofür wird er verwendet?
Der Bland-Altman-Plot ist ein grafisches Werkzeug, um die Übereinstimmung zwischen zwei Messmethoden zu bewerten. Anstatt nur eine Korrelation oder lineare Regression zu berechnen, veranschaulicht er die Differenzen zwischen zwei Messungen in Abhängigkeit von ihrem Mittelwert.
Formelle Beschreibung:
Für zwei Messmethoden und wird für jedes Datenpaar berechnet:
- Mittelwert:
- Differenz:
Diese Werte werden im Plot mit auf der x-Achse und auf der y-Achse dargestellt.Metapher zur Veranschaulichung:
Stell dir vor, du hast zwei Uhren, die du nutzt, um die Zeit zu messen:
- Der Mittelwert entspricht der “durchschnittlichen Zeit” der beiden Uhren.
- Die Differenz zeigt, wie stark die beiden Uhren voneinander abweichen.
Wenn beide Uhren gut synchronisiert sind, sind die Differenzen klein, unabhängig von der Zeit.Wichtigkeit des Bland-Altman-Plots:
- Der Plot hilft, systematische Abweichungen (Bias) zwischen den Methoden zu erkennen, z. B. ob eine Methode stets größere Werte liefert.
- Er zeigt, ob die Abweichungen konstant oder variabel über den Messbereich sind.
- Zusätzlich werden oft die Grenzen der Übereinstimmung (Limits of Agreement, LoA) eingezeichnet: Dies gibt an, in welchem Bereich 95 % der Differenzen liegen.
Beispiel:
Zwei Methoden messen die Körpertemperatur:
- Methode A liefert die Werte
- Methode B liefert die Werte
Mittelwerte:
Differenzen:
Ein Bland-Altman-Plot zeigt die Mittelwerte auf der x-Achse und die Differenzen auf der y-Achse, wodurch wir auf einen Blick sehen können, wie gut die beiden Methoden übereinstimmen.Frage eines Studierenden:
“Warum verwenden wir Bland-Altman und nicht die Korrelation, um Übereinstimmung zu messen?”Antwort:
Die Korrelation misst die lineare Beziehung zwischen zwei Variablen, nicht die Übereinstimmung. Zwei Methoden können hoch korreliert sein, aber systematische Abweichungen aufweisen. Der Bland-Altman-Plot zeigt explizit, wie die Messungen voneinander abweichen und ob diese Abweichungen zufällig oder systematisch sind.
install.packages("BlandAltmanLeh")
install.packages("ggplot2")
library(BlandAltmanLeh)
library(ggplot2)
plot <- bland.altman.plot(method_A, method_B, graph.sys = "ggplot2")
print(plot + xlab("Mittelwert der Messungen") + ylab("Mittelwertdifferenz")
+ ggtitle("Bland-Altman-Plot")
+theme(plot.title=element_text(hjust = 0.5)))+theme_bw()+geom_hline(yintercept = 0, color = "orange", size = 1)
Output
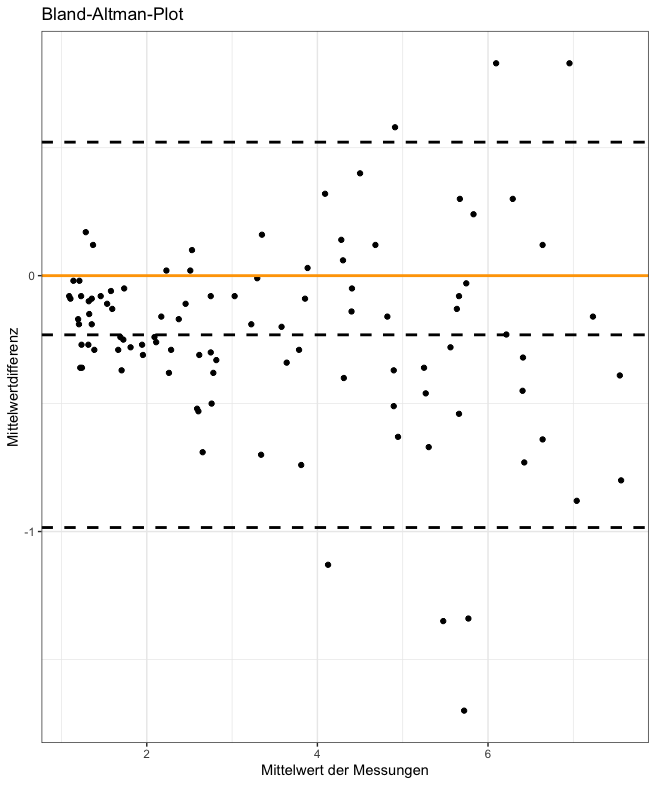
Im Mittel liegen die Messwerte von B etwa 0.25 über den Messwerten von A. Übereinstimmungsgrenzen: von circa -1 bis circa 0.5 d.h. für 95% der Fälle ist der Messwert für A zwischen ca. 1 kleiner und 0.5 größer als der Messwert von B
Anstieg der Variation der Messdifferenzen mit zunehmenden Mittelwert, somit sind die Übereinstimmungsgrenzen nicht für den gesamten Wertebereich repräsentativ
#Aufgabe 2c (extra overkill)
# Lade die notwendigen Bibliotheken
library(BlandAltmanLeh)
library(ggplot2)
# Berechne die Differenzen und den Mittelwert der Messungen
differences <- method_A - method_B
means <- (method_A + method_B) / 2
# Berechne den Mittelwert und die Standardabweichung der Differenzen
mean_diff <- mean(differences, na.rm = TRUE)
sd_diff <- sd(differences, na.rm = TRUE)
# Berechne die Grenzen der Übereinstimmung (±1.96 Standardabweichungen)
upper_limit <- mean_diff + 1.96 * sd_diff
lower_limit <- mean_diff - 1.96 * sd_diff
# Erstelle einen Datenrahmen für ggplot2
data <- data.frame(Means = means, Differences = differences)
# Bestimme die Grenzen für die Textplatzierung
x_position <- min(means, na.rm = TRUE) + (max(means, na.rm = TRUE) - min(means, na.rm = TRUE)) * 0.05 # 5% vom linken Rand
# Erstelle den Bland-Altman-Plot mit ggplot2 und Textbeschriftungen
plot <- ggplot(data, aes(x = Means, y = Differences)) +
geom_point(color = "blue", alpha = 0.6) +
geom_hline(yintercept = mean_diff, color = "red", size = 1) +
geom_hline(yintercept = upper_limit, linetype = "dashed", color = "orange", size = 1) +
geom_hline(yintercept = lower_limit, linetype = "dashed", color = "orange", size = 1) +
xlab("Mittelwert der Messungen") +
ylab("Differenz der Messungen") +
ggtitle("Bland-Altman-Plot") +
theme_bw() +
theme(
plot.title = element_text(hjust = 0.5)
) +
# Hinzufügen von Textbeschriftungen mit dynamischer x-Position
annotate("text",
x = x_position,
y = mean_diff,
label = paste("Mittelwert:", round(mean_diff, 2)),
color = "red",
hjust = 0,
vjust = -0.5,
size = 4) +
annotate("text",
x = x_position,
y = upper_limit,
label = paste("Obere Grenze:", round(upper_limit, 2)),
color = "orange",
hjust = 0,
vjust = -0.5,
size = 4) +
annotate("text",
x = x_position,
y = lower_limit,
label = paste("Untere Grenze:", round(lower_limit, 2)),
color = "orange",
hjust = 0,
vjust = 1.5,
size = 4)
# Drucke den Plot
print(plot)
# Definiere den akzeptablen Bias
akzeptabler_bias <- 1.0 # Beispielwert, passe ihn an deine Bedürfnisse an
# Interpretation der Ergebnisse
cat("### Interpretation der Bland-Altman-Analyse ###\n\n")
# 1. Mittelwert der Differenzen
cat(sprintf("**Mittelwert der Differenzen (Bias):** %f\n", mean_diff))
cat("Der Bias zeigt den durchschnittlichen Unterschied zwischen den beiden Messmethoden.\n\n")
# 2. Grenzen der Übereinstimmung
cat(sprintf("**Obere Grenze der Übereinstimmung:** %f\n", upper_limit))
cat(sprintf("**Untere Grenze der Übereinstimmung:** %f\n", lower_limit))
cat("Die Grenzen der Übereinstimmung (Limits of Agreement) geben den Bereich an, in dem 95% der Differenzen zwischen den beiden Methoden liegen.\n\n")
# 3. Bewertung des Bias
if(abs(mean_diff) < akzeptabler_bias) {
cat("**Bewertung des Bias:**\nDer Bias ist gering und möglicherweise klinisch nicht relevant.\n\n")
} else {
cat("**Bewertung des Bias:**\nDer Bias ist signifikant und könnte klinisch relevant sein.\n\n")
}
# 4. Überprüfung auf proportionalen Bias
# Führe eine lineare Regression durch, um zu prüfen, ob die Differenzen vom Mittelwert abhängen
model <- lm(Differences ~ Means, data = data)
p_value <- summary(model)$coefficients[2,4]
cat("**Proportionaler Bias:**\n")
if(p_value < 0.05) {
cat(sprintf("Es gibt einen signifikanten proportionalen Bias (p = %f). Die Differenzen hängen vom Mittelwert der Messungen ab.\n\n", p_value))
} else {
cat(sprintf("Es gibt keinen signifikanten proportionalen Bias (p = %f). Die Differenzen hängen nicht vom Mittelwert der Messungen ab.\n\n", p_value))
}
# 5. Zusammenfassung
cat("### Zusammenfassung ###\n")
cat(sprintf("Der Bland-Altman-Plot zeigt einen durchschnittlichen Bias von %f Einheiten zwischen Methode A und Methode B.\n", mean_diff))
cat(sprintf("Die 95-Limits der Übereinstimmung liegen zwischen %f und %f Einheiten.\n", lower_limit, upper_limit))
if(p_value < 0.05) {
cat("Es besteht ein signifikanter proportionaler Bias, was darauf hindeutet, dass die Differenzen je nach Messwert variieren.\n")
} else {
cat("Es besteht kein signifikanter proportionaler Bias, was darauf hindeutet, dass die Differenzen unabhängig vom Messwert sind.\n")
}
Antwort:
Vor der log-Transformation:
- Die Mittelwertdifferenz beträgt -0.23, was auf eine moderate systematische Abweichung zwischen den Messmethoden hinweist.
- Die Grenzen der Übereinstimmung liegen bei 0.52 (obere Grenze) und -0.98 (untere Grenze). Der Bereich der Abweichungen ist relativ groß.
- Bei höheren Mittelwerten scheinen die Differenzen stärker zu streuen, was darauf hinweist, dass die Übereinstimmung der Methoden mit steigenden Werten abnimmt.
Nach der log-Transformation:
- Die Mittelwertdifferenz ist auf -0.08 reduziert, was auf eine deutlich bessere Übereinstimmung zwischen den Methoden hinweist.
- Die Grenzen der Übereinstimmung sind enger zusammen: 0.11 (obere Grenze) und -0.27 (untere Grenze). Dies zeigt, dass die Streuung der Differenzen nach der log-Transformation abgenommen hat.
- Die Punkte sind gleichmäßiger verteilt, und extreme Abweichungen bei höheren Werten wurden abgeschwächt.
Interpretation:
Die log-Transformation hat die Unterschiede zwischen den Messmethoden reduziert und die Streuung der Differenzen deutlich verringert. Dies deutet darauf hin, dass die log-transformierten Daten eine bessere Vergleichbarkeit der Messmethoden liefern, insbesondere bei höheren Messwerten. Die log-Transformation ist hier ein sinnvoller Schritt, um die Übereinstimmung der Methoden zu verbessern.
Meine kritische Betrachtung (extra)
Kritische Betrachtung der Log-Transformation im Bland-Altman-Plot
Die Log-Transformation ist ein mathematischer Ansatz, um Daten zu skalieren und die Variabilität der Abweichungen zu reduzieren. Sie wird häufig angewandt, wenn die Streuung der Differenzen zwischen zwei Messmethoden proportional zu den Messwerten zunimmt (Heteroskedastizität).
Was macht die Log-Transformation?
Sie skaliert die Daten so, dass große Abweichungen bei höheren Werten abgeschwächt werden. Dies führt zu engeren Grenzen der Übereinstimmung und einer scheinbar besseren Übereinstimmung zwischen den Methoden.Kritische Punkte zur Log-Transformation:
- Voraussetzungen prüfen: Eine Log-Transformation ist nur sinnvoll, wenn die Variabilität der Differenzen mit dem Messwert steigt. Ohne diese Voraussetzung kann die Transformation zu einer verzerrten Darstellung führen.
- Reduktion der Streuung: Nach der Transformation wirken die Differenzen kleiner und die Grenzen der Übereinstimmung enger. Dies kann den Eindruck erwecken, dass die Methoden besser übereinstimmen, obwohl die ursprünglichen Differenzen unverändert bleiben.
- Kommunikation der Transformation: Es muss transparent gemacht werden, dass eine Transformation angewandt wurde und warum sie notwendig war. Eine unreflektierte Anwendung kann zu einer irreführenden Interpretation führen.
Metapher zur Veranschaulichung:
Stell dir vor, du betrachtest zwei Personen, die unterschiedlich schnell laufen:
- Ohne Transformation siehst du die absolute Geschwindigkeit beider Läufer. Die Unterschiede erscheinen groß.
- Nach der Log-Transformation betrachtest du die prozentuale Geschwindigkeit im Verhältnis zur Strecke. Die Unterschiede erscheinen kleiner.
Die “Wahrheit” bleibt gleich, aber der Blickwinkel hat sich verändert.Frage eines Studierenden:
“Ist die log-Transformation hier gerechtfertigt oder manipuliert sie die Ergebnisse?”Antwort:
Die Log-Transformation ist gerechtfertigt, wenn sie hilft, proportionale Abweichungen korrekt darzustellen und Heteroskedastizität zu reduzieren. Wenn jedoch keine klaren Gründe für die Transformation vorliegen, kann sie zu einer Verschönerung der Ergebnisse führen. In solchen Fällen sollten die Daten sowohl vor als auch nach der Transformation betrachtet und kritisch interpretiert werden.
Aufgabe 3
Als „Beer Binger” bezeichnet man eine Person, die für gewöhnlich sechs oder mehr Flaschen Bier innerhalb kurzer Zeit trinkt. Die folgende Tabelle zeigt die Daten einer Zufallsstichprobe von Männern mittleren Alters, die in Kuopio (Finnland) aufgenommen wurden (Kauhanen et al., 1997). Zu Beginn der Studie wurde für die Zufallsstichprobe erfasst, ob es sich um einen „Beer Binger” handelte. Zudem wurde für jede Person nach ca. 8 Jahren basierend auf Totenscheinen erhoben, ob ein kardiovaskulär bedingter Tod eingetreten ist.
| Beer Binger | ||
|---|---|---|
| nein | ja | |
| Kardiovaskulär bedingter Tod nein | 1519 | 63 |
| Kardiovaskulär bedingter Tod ja | 52 | 7 |
(a) Schätzen Sie das Risiko für kardiovaskulär bedingten Tod für Beer Binger und für Nicht-Beer-Binger.
Weitere Hilfreiche Referenz
Beer Binger
Nicht Beer Binger
(b) Schätzen Sie das relative Risiko für kardiovaskulär bedingten Tod für Beer Binger im Vergleich zu Nicht-Beer-Bingern und interpretieren Sie das relative Risiko.
*Wenn man die jeweiligen Zellen einer Vierfeldertafel mit A,B,C,D benennt/einteilt.
Interpretation des relativen Risikos
- RR = 1: Das Risiko für das Ereignis ist für die exponierte Gruppe und die nicht-exponierte Gruppe gleich hoch.
- RR > 1: Das Risiko der exponierten Gruppe ist größer als das Risiko der nicht-exponierten Gruppe; Nachweis eines positiven Zusammenhangs/eines möglichen kausalen Faktors.
- RR < 1: Das Risiko der exponierten Gruppe ist niedriger als das Risiko der nicht-exponierten Gruppe; Nachweis eines negativen Zusammenhangs/möglicher protektiver Faktor.
Berechnung
Das relative Risiko (RR) quantifiziert das Verhältnis des Risikos für ein Ereignis (hier: kardiovaskulär bedingter Tod) in einer exponierten Gruppe (Beer Binger) im Vergleich zu einer nicht-exponierten Gruppe (Nicht-Beer-Binger).
Basierend auf den in Aufgabe (a) berechneten absoluten Risiken ergibt sich:
ARBeer Binger: 0.1
ARNicht-Beer-Binger: 0.033
Die Berechnung des relativen Risikos erfolgt mittels Division des absoluten Risikos der exponierten Gruppe durch das absolute Risiko der nicht-exponierten Gruppe:
Interpretation:
Das relative Risiko von 3.03 impliziert, dass das Risiko eines kardiovaskulär bedingten Todes bei Beer Bingern etwa 3.03-mal so hoch ist wie bei Nicht-Beer-Bingern. Da das RR größer als 1 ist, deutet dies auf einen positiven Zusammenhang zwischen Beer Binging und dem Risiko eines kardiovaskulär bedingten Todes hin. Beer Binging kann als potenzieller kausaler Risikofaktor interpretiert werden.
→ Gemäß der Schätzung ist das Risiko, einen Kardiologisch bedingten Tod zu erleiden, für Beer Binger ca 3 mal so hoch wie für nicht Beer Binger
(c) Geben Sie ein 95% Konfidenzintervall für das relative Risiko an.
Da das relative Risiko (RR) nicht normalverteilt ist, wird zunächst das 95%-Konfidenzintervall (KI) für den natürlichen Logarithmus des RR (ln(RR)) berechnet und anschließend mittels Exponentialfunktion in das 95%-KI für das RR transformiert.
1. Berechnung des Standardfehlers von ln(RR):
2. Berechnung des 95%-KI für ln(RR):
Untere Grenze:
Obere Grenze:
3. Transformation in das 95%-KI für RR:
Untere Grenze:
Obere Grenze:
Ergebnis: Das 95%-Konfidenzintervall für das relative Risiko beträgt [1.423, 6.417].
Interpretation: Mit 95%iger Sicherheit liegt das wahre relative Risiko zwischen 1.423 und 6.417. Da dieses Intervall den Wert 1 nicht einschließt, ist der beobachtete Zusammenhang zwischen Beer Binging und kardiovaskulär bedingtem Tod statistisch signifikant (p < 0.05). Dies deutet darauf hin, dass Beer Binging mit hoher Wahrscheinlichkeit das Risiko für kardiovaskulär bedingte Todesfälle erhöht.
Aufgabe 4
In einer Studie soll untersucht werden ob es einen Zusammenhang zwischen Geburtsgewicht und verzögerter Entwicklung gibt. Innerhalb einer 6-monatigen Zeitspanne wurden alle Kinder in Epidoria mit einem geringen Geburtsgewicht über 3 Jahre verfolgt. Repräsentative Kontrollen (Kinder mit normalem Geburtsgewicht) wurden ebenfalls über 3 Jahre hinweg untersucht. Sobald die Kinder ihr drittes Lebensalter erreicht hatten, wurde der Entwicklungsstand der Kinder anhand eines Tests über charakterliche/soziale, sprachliche und motorische Fähigkeiten erfasst. Zudem wurde für jedes Kind der Blutspiegel des Schwermetalls Blei (Blutbleispiegel) gemessen. Folgende Tabelle zeigt die Daten.
| Niedriger Blutbleispiegel | Niedriger Blutbleispiegel | Hoher Blutbleispiegel | Hoher Blutbleispiegel | |||
|---|---|---|---|---|---|---|
| Normales Gew. | Niedriges Gew. | ∑ | Normales Gew. | Niedriges Gew. | ∑ | |
| normale Entw. | 235 | 135 | 370 | 48 | 85 | 133 |
| verzögerte Entw. | 53 | 52 | 105 | 24 | 88 | 112 |
| ∑ | 288 | 187 | 475 | 72 | 173 | 245 |
(a) Schätzen Sie das Odds Ratio für den Zusammenhang zwischen Geburtsgewicht und Entwicklung für die Gesamtpopulation und geben Sie ein 95% Konfidenzintervall an.
Berechnung des Odds Ratio (OR) für die Gesamtpopulation:
Schwierigkeiten mit OR? → Odds Ratio verstehen und berechnen
Zuerst fassen wir die Daten zusammen, unabhängig vom Blutbleispiegel:
Die Odds Ratio berechnet sich wie folgt:
wobei:
- = Anzahl der Personen mit normalem Gewicht und normaler Entwicklung = 283
- = Anzahl der Personen mit normalem Gewicht und verzögerter Entwicklung = 77
- = Anzahl der Personen mit niedrigem Gewicht und normaler Entwicklung = 220
- = Anzahl der Personen mit niedrigem Gewicht und verzögerter Entwicklung = 140
Berechnung des 95%-Konfidenzintervalls (KI) für das OR:
Da das OR nicht normalverteilt ist, berechnen wir zunächst das 95%-KI für den natürlichen Logarithmus des OR () und transformieren dieses anschließend in das 95%-KI für das OR.
1. Standardfehler von :
2. 95%-KI für :
Untere Grenze: Obere Grenze:
3. Transformation in das 95%-KI für OR:
Untere Grenze: Obere Grenze:
Ergebnis: Das 95%-Konfidenzintervall für das Odds Ratio der Gesamtpopulation beträgt [1.682, 3.251].
(b) Schätzen Sie das Odds Ratio für Kinder mit niedrigem Blutbleispiegel und das Odds Ratio für Kinder mit hohem Blutbleispiegel.
Niedriger Blutbleispiegel:
Hoher Blutbleispiegel:
(c) Vergleichen Sie die Odds Ratios für Gesamtpopulation und einzelne Gruppen. Was fällt auf?
Auffälligkeiten:
- Alle drei Odds Ratios sind größer als 1, was darauf hindeutet, dass ein niedriges Geburtsgewicht in allen Gruppen mit einer erhöhten Odds für eine verzögerte Entwicklung assoziiert ist.
- Das Odds Ratio für die Gesamtpopulation () ist höher als das Odds Ratio für Kinder mit niedrigem Blutbleispiegel () und leicht höher als das Odds Ratio für Kinder mit hohem Blutbleispiegel ().
- Das Odds Ratio für Kinder mit hohem Blutbleispiegel ist höher als das für Kinder mit niedrigem Blutbleispiegel.
Interpretation:
Der Blutbleispiegel scheint ein Confounder (Störfaktor) zu sein, der den Zusammenhang zwischen Geburtsgewicht und Entwicklung beeinflusst. Wenn der Blutbleispiegel nicht berücksichtigt wird (Gesamtpopulation), wird der Effekt des niedrigen Geburtsgewichts überschätzt.
Zudem deutet der höhere darauf hin, dass ein hoher Blutbleispiegel möglicherweise einen stärkeren negativen Effekt auf die Odds für eine verzögerte Entwicklung bei niedrigem Geburtsgewicht hat als ein niedriger Blutbleispiegel. Dies könnte auf eine Interaktion (Effektmodifikation) zwischen Geburtsgewicht und Blutbleispiegel hinweisen.