r# Aufgabe 1 (16 Punkte)

Die folgende Graphik zeigt die Odds Ratios, die in zwei verschiedenen Studien (einer randomisierten kontrollierten Studie, der sogenannten Heart Protection Study, und der Beobachtungsstudie EPIC) geschätzt wurden bezüglich des Zusammenhangs zwischen Vitamin C und kardiovaskulären Erkrankungen. Das Odds Ratio für Vitamin C wurde in der EPIC Studie getrennt für Männer und Frauen basierend auf folgendem logistischen Regressionsmodell geschätzt:

P (Y_{i} = 1∣ X_{1 i} = x_{1 i}, X_{2 i} = x_{2 i}, X_{3 i} = x_{3 i}) = \frac{exp ( β _{0} + β _{1} x _{1 i} + β _{2} x _{2 i} + β _{3} x _{3 i} )}{1 + exp ( β _{0} + β _{1} x _{1 i} + β _{2} x _{2 i} + β _{3} x _{3 i} )}

wobei $x_{1 i}$ die Vitamin C Konzentration in $μ mol / L$ Plasma, $x_{2 i}$ das Alter und $x_{3 i}$ den Raucherstatus des Individuums $i$ angibt.

In der Heart Protection Study wurde das Odds Ratio für Vitamin C basierend auf folgendem logistischen Regressionsmodell geschätzt:

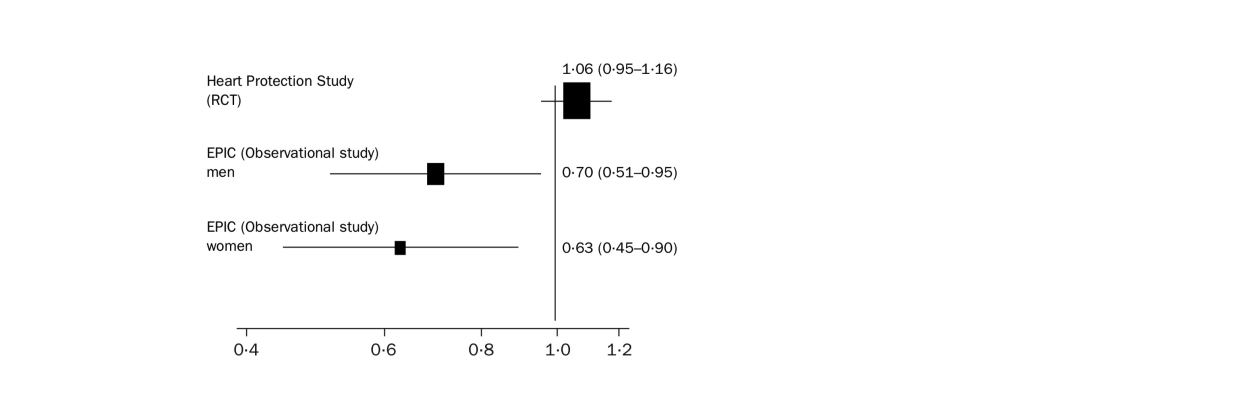
P (Y_{i} = 1∣ X_{1 i} = x_{1 i}) = \frac{exp ( β _{0} + β _{1} x _{1 i} )}{1 + exp ( β _{0} + β _{1} x _{1 i} )}

(a) Interpretieren Sie die drei Odds Ratios. (3 Punkte)

Zunächst einmal beschreiben alle drei dargestellten Odds Ratios den Zusammenhang zwischen Vitamin C und kardiovaskulären Erkrankungen in zwei verschiedenen Studien

Heart Protection Study
- Odds Ratio: 1.06 (95%-KI:0.95-1.16)
- Interpretation: Aufgrund des OR von 1.06 kann man sagen, dass laut Studie eine höhere Vitamin-C-Konzentration mit einem leicht erhöhten Risiko für kardiovaskuläre Erkrankungen assoziiert ist
- Da das KI die 1 enthält, ist dieser Effekt aber nicht besonders statistisch signikifant. Es gibt dementsprechend keinen signifikanten Effekt dafür, dass Vitamin C das Risiko beeinflusst
EPIC (men)
- Odds Ratio 0.70 (95%-KI:0.51-0.95)
- Interpretation: Aufgrund des OR von 0.70 kann man sagen, dass eine höhere Vitamin-C-Konzentration mit einem 30% geringeren Risiko für kardiovaskuläre Erkrankungen bei Männern assoziiert wird. in EPIC wurde für Alter und Rauchen adjustiert.
- Das KI (0.51-0.95) liegt unter 1 und ist damit statistisch signifikant. Dies spricht für einen schützenden Effekt von Vitamin C bei Männern
EPIC (women)
- Odds Ratio 0.63 (95%-KI:0.45-0.90)
- Interpretation: Die OR beträgt 0.63 damit ist eine höhere Vitamin-C-Konzentration mit einem 37% geringeren Risiko für kardiovaskuläre Erkrankungen bei Frauen verbunden
- Das Konfidenzintervall liegt unter 1 und damit ist die OR statistisch signifikant. Auch dies spricht für einen schützenden Effekt von Vitamin C bei Frauen

(b) Geben Sie für die Heart Protection Study den Regressionskoeffizienten $β_{1}$ und das zugehörige Konfidenzintervall an. (2 Punkte)

Beziehung zwischen OR und $\beta_1$

$OR = e^{β_{1}}$
Durch Umformen:
$β_{1 =} ln (OR)$

β_{1} = ln (1.06) = 0.05827

Konfidenzintervall

ln (0.95) ln (1.16) = - 0.05129 = 0.14842

(c) Erklären Sie, wieso die Odds Ratio in der Beobachtungsstudie und in der randomisierten kontrollierten Studie nicht beide mit dem ersten logistischen Regressionsmodell geschätzt wurden. (2 Punkte)

In RCTs werden Confounder durch Randomisierung kontrolliert, sodass sie im Mittel gleichverteilt sind. Daher reicht ein einfaches Modell ohne Adjustierung.
In Beobachtungsstudien fehlt diese Randomisierung, weshalb Confounder explizit im Modell berücksichtigt werden müssen.
In der Beobachtungsstudie sind Confounder vorhanden die im Modell berücksichtigt werden müssen
In der randomisierten kontrollierten Studie sind potenzielle Confounder größtenteils schon ausgeglichen, sodass ein einfacheres Modell reicht.
Zudem werden einmal Expositionen unterschiedblich behandelt, einmal beobachtete Variable vs. zufällige Zuweisung

(d) Welche Alternativen gibt es im Allgemeinen, um für Confounding zu adjustieren? Nennen Sie mindestens drei Alternativen zu einem multiplen Regressionsmodell. (3 Punkte)

Während der Datenanalyse

Stratifizierung: Aufteilung der Daten in homogene Subgruppen basierend auf den Confoundern und Analyse innerhalb dieser Subgruppen
Standardisierung: Anpassung der Daten an eine Referenzpopulation, um Unterschiede in den Confoundern auszugleichen
Propensity-Score-Methoden: Schätzung der Wahrscheinlichkeit einer Behandlung basierend auf den Confoundern und Anpassung der Analyse entsprechend, um verzerrende Effekte zu minimieren

Die untenstehenden wären keine legitime Antwort, da sie Desing-Maßnahmen und keine Analysemethoden sind

Während der Studienplanung

Zufällige Einteilung der Studienteilnehmer in Behandlungsgruppen um sicherzustellen, dass Confounder gleichmäßig verteilt sind. Dadurch wird die Verzerrung durch unbeabsichtigte Störfaktoren minimiert

Ausschluss von Studienteilnehmern, die bestimmte Confounder aufweisen, um deren Einfluss zu minimieren

Matching also die Paarung von Studienteilnehmern in verschiedenen Gruppen mit ähnlichen Werten der Confounder. Dadurch wird die Verteilung der Confounder zwischen den Gruppen ausgeglichen

(e) Welche Ernährungsempfehlungen würden Sie aufgrund des Ergebnisses der randomisierten klinischen Studie treffen, welche basierend auf den Ergebnissen der Beobachtungsstudie? (2 Punkte)

Randomisierte Klinische Studie:

Ein OR von 1.06 mit KI [0.95, 1.16] zeigt keinen signifikanten Effekt – weder schädlich noch nützlich.

Beobachtungsstudie:

höhere Vitamin-C Zunahme ist zu empfehlen, da diese die Wahrscheinlichkeit für kardiovaskulären Problemen bei Männern und bei Frauen beträchtlich senkt

→ Randomisierte kontrollierte Studien (RCTs), die als Goldstandard in der klinischen Forschung gelten, haben keinen eindeutigen Nutzen von Vitamin C nachgewiesen. Beobachtungsstudien wie die EPIC-Studie können lediglich Assoziationen aufzeigen, jedoch keine kausalen Zusammenhänge belegen. Daher ist eine Empfehlung für die alleinige Einnahme von Vitamin C auf der Grundlage von Beobachtungsstudien wie EPIC nicht gerechtfertigt.

(f) Was könnten mögliche Gründe für die Diskrepanz zwischen den Ergebnissen der zwei Studien sein? (2 Punkte)

Confounder, In EPIC wurden nur Alter und Rauchen adjustiert – andere Confounder (z.B. sozioökonomischer Status, Gesamternährung) bleiben möglicherweise unberücksichtigt.
Verschiedene Populationsmengen/Studienteilnehmer, dementsprechend nicht die gleichen Bedingungen
Zusätzliche Gründe:
- Reverse Kausalität: In Beobachtungsstudien könnten niedrige Vitamin-C-Spiegel Folge (nicht Ursache) von Erkrankungen sein.
- Dosisunterschiede: RCTs testen oft Supplemente, Beobachtungsstudien messen natürliche Spiegel.

(g) Unter Berücksichtigung der Gründe für die Diskrepanz zwischen den Ergebnissen der randomisierten klinischen Studie und der Beobachtungsstudie, argumentieren Sie ob Vitamin C kardiovaskulären Krankheiten vorbeugen kann. (2 Punkte)

Die Diskrepanz zwischen den Studien lässt sich durch die unterschiedliche Aussagekraft der Studiendesigns erklären:

Randomisierte klinische Studie (RCT):
- Als Goldstandard der Kausalitätsprüfung minimiert die Randomisierung Confounding. Das nicht-signifikante OR von 1.06 (KI inklusive 1) zeigt keinen kausalen Effekt von Vitamin C auf kardiovaskuläre Erkrankungen.
- Selbst bei hoher statistischer Power (typisch für große RCTs wie die Heart Protection Study) wurde kein Nutzen nachgewiesen. Dies spricht stark gegen eine präventive Wirkung.
Beobachtungsstudie (EPIC):
- Die signifikanten ORs (0.70 bei Männern, 0.63 bei Frauen) deuten auf eine Assoziation hin, jedoch keine Kausalität.
- Trotz Adjustierung für Alter und Rauchen bleiben Residual-Confounder plausibel (z.B. ballaststoffreiche Ernährung, körperliche Aktivität, sozioökonomischer Status), die sowohl mit höheren Vitamin-C-Spiegeln als auch mit geringerem Erkrankungsrisiko korrelieren.
- Zudem könnten niedrige Vitamin-C-Spiegel eine Folge (nicht Ursache) bereits bestehender Risikofaktoren sein (reverse Kausalität).

Fazit:
Es gibt keine Evidenz für einen präventiven Effekt von Vitamin C. Die Assoziation in der Beobachtungsstudie ist wahrscheinlich auf Störfaktoren zurückzuführen. Somit gibt es keine Evidenz dafür, dass Vitamin C kardiovaskulären Krankheiten vorbeugt.

Die untenstehenden wären keine legitime Antwort

Aus der Beobachtungsstudie ist eher anzunehmen, dass Vitamin C kardiovaskulären Krankheiten vorbeugen kann, da die beobachteten Ergebnisse eine statistische Signifikanz aufeisen ( $OR < 1$ ), wobei bei der randomisierten Kontrollstudie keine statistische Signifikanz vorliegt ( $OR > 1$ )

Aufgabe 2 (17 Punkte)

In einer Studie von Myles et al. 1996 wird untersucht, inwieweit die Menge an zugeführtem Sauerstoff ( $D O_{2}$ ) die Sauerstoffaufnahme von Patienten bei Herzoperationen beeinflusst. Bei jedem der $n = 20$ Patienten in der Studie wurde dabei die Sauerstoffaufnahme mit zwei verschiedenen Methoden ermittelt: einmal durch Analyse der ausgeatmeten Luft ( $V O_{2 G}$ ) und einmal mithilfe des inversen Fickschen Prinzips ( $V O_{2 F}$ ).

(a) Zeichnen Sie (nur) das erste Messpaar mit $V O_{2 G} = 144$ ml/min und $V O_{2 F} = 153$ ml/min in einen Bland-Altman-Plot zum Vergleich der beiden Messmethoden ein. Beschriften Sie dazu auch den Plot und verwenden Sie manche der unten angegebenen Stichprobenmittel/Standardabweichungen, um die zum Plot gehörigen Markierungen einzuzeichnen. (8 Punkte)

Gegebene Werte:
Stichprobenmittel: $\overline{V O}_{2 G} = 164$ ; $\overline{V O}_{2 F} = 194$
Standardabweichungen: $S D (V O_{2 G}) = 28$ ; $S D (V O_{2 F}) = 51$ ; $S D (V O_{2 G} + V O_{2 F}) = 70$ ; $S D (V O_{2 G} - V O_{2 F}) = 43$

X-Achse: Der Mittelwert der beiden Messmethoden pro Datenpunkt:
$Mittelwert = \frac{Messung _{A} + Messung _{B}}{2} = \frac{V O _{2 G} + V O _{2 F}}{2} = \frac{144 \frac{ml}{min} + 153 \frac{ml}{min}}{2} = 148.5 \frac{ml}{min}$
Y-Achse: Die Differenz zwischen den beiden Messmethoden:
$Differenz = Messung_{A} - Messung_{B} = 144 \frac{ml}{min} - 153 \frac{ml}{min} = (- 9 \frac{ml}{min})$
Horizontale Linien:
- Mittlere Differenz (Bias): $\overset{ˉ}{d} = \overline{V O}_{2 G} - \overline{V O}_{2 F} = 164 \frac{ml}{min} - 194 \frac{ml}{min} = (- 30 \frac{ml}{min})$
- Grenzen der Übereinstimmung (Limits of Agreement, LoA):

LoA = \overset{ˉ}{d} \pm 1.96 \cdot SD (d) = - 30 \pm 1.96 \cdot S D (V O_{2 G} - V O_{2 F}) = - 30 \pm 1.96 \cdot 43 = [- 114.28, 54.28]

Achtung: Verwechslungsgefahr bei Standardabweichungen!

Warum wir $S D (V O_{2 G} - V O_{2 F}) = 43$ verwenden und nicht $S D (V O_{2 G} + V O_{2 F}) = 70$ :

Kern des Bland-Altman-Plot:
Es geht um die Übereinstimmung der Methoden, d. h. um die Differenzen zwischen $V O_{2 G}$ und $V O_{2 F}$ .
Die Limits of Agreement (LoA) quantifizieren, wie stark diese Differenzen streuen – dafür ist $S D (V O_{2 G} - V O_{2 F})$ entscheidend.

Folgen einer falschen SD:
Mit $S D (V O_{2 G} + V O_{2 F}) = 70$ würdest du die Variabilität der Summe (nicht der Differenz!) einbeziehen.
Dies würde die LoA falsch berechnen und zu irreführenden Schlüssen führen (z. B. zu breite/schmale Grenzen).

Mathematischer Hintergrund:
Die Varianz der Differenz hängt von der Kovarianz der Methoden ab: $Var (A - B) = Var (A) + Var (B) - 2 \cdot Cov (A, B)$ Die Summen-Standardabweichung ist hier irrelevant.

🔍 Warum steht $S D (V O_{2 G} + V O_{2 F})$ dann in der Aufgabe?
– Um zu prüfen, ob du den Kontext verstehst!
– Sie könnte für andere Analysen (z. B. Korrelation) nützlich sein – nicht aber für LoA.

Beispielplot (schematisch)

Differenz (VO₂G - VO₂F)
  ^
  |                          o (148.5, -9)
  |
  |---------------------------------------------------- y = 54.28 (Obere LoA)
  |
  |
  |---------------------------------------------------- y = -30 (Bias)
  |
  |
  |---------------------------------------------------- y = -114.28 (Untere LoA)
  +--------------------------------------------------------------------->
    100          150          200          Mittelwert von VO₂G und VO₂F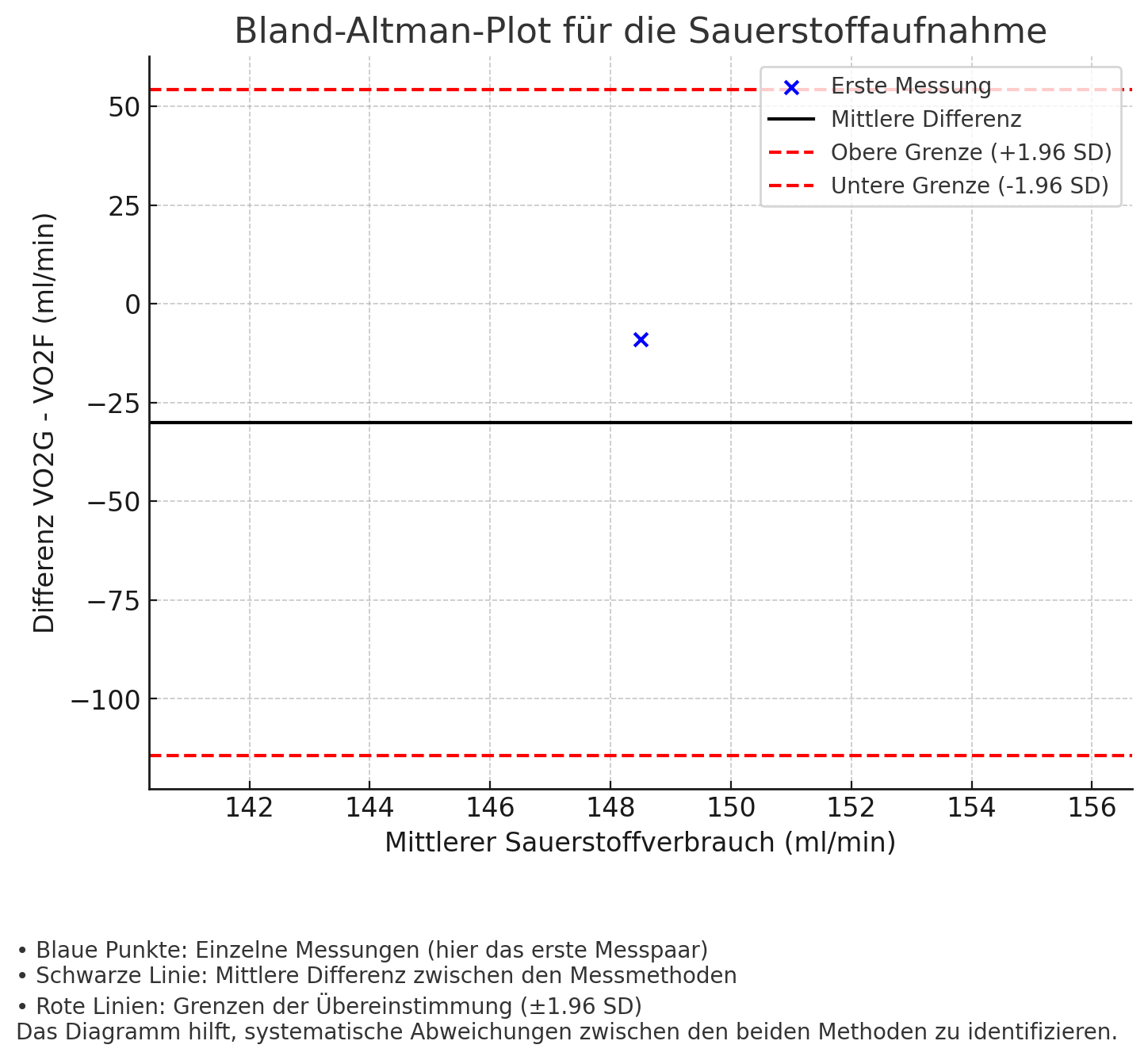

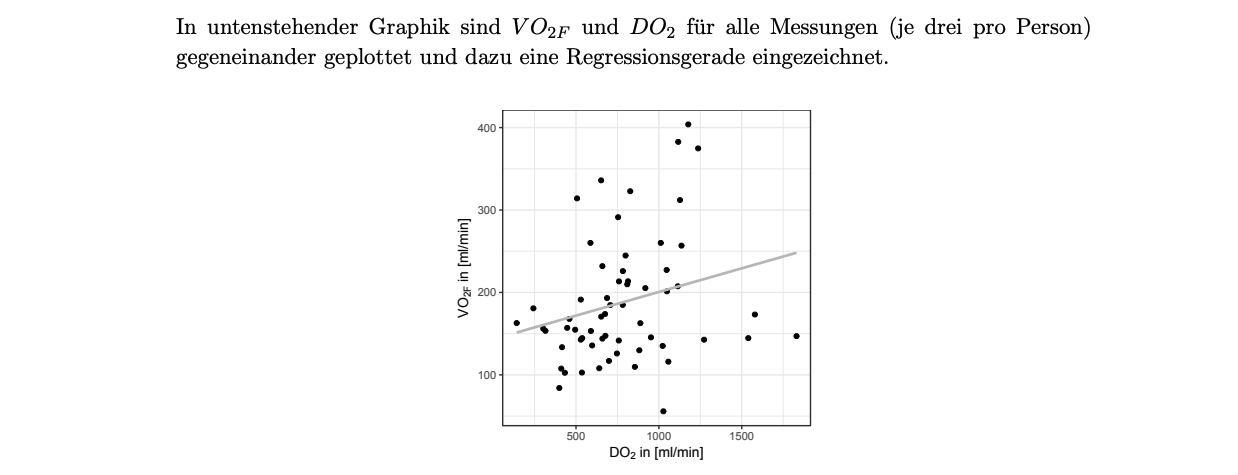
(b) Welcher der vier Werte entspricht $r_{V D}$ , dem Korrelationskoeffizienten nach Bravais-Pearson von $V O_{2 F}$ und $D O_{2}$ ? Begründen Sie kurz Ihre Entscheidung. (3 Punkte)

A) $r_{V D} = 0.25$
B) $r_{V D} = 0.85$
C) $r_{V D} = - 0.25$
D) $r_{V D} = - 0.85$

Beispiele für verschiedene Bravais-Pearson Werte

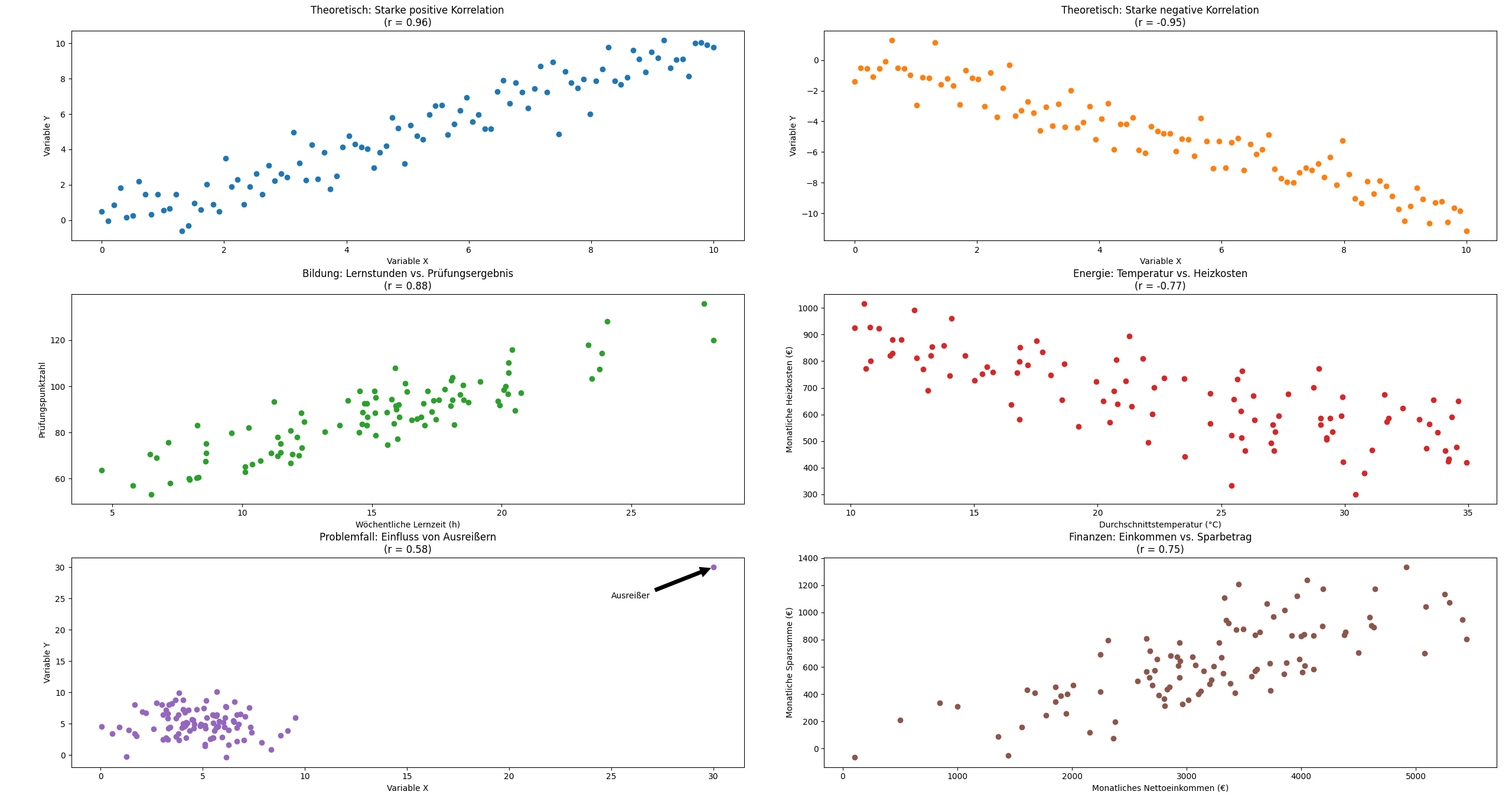
Für mehr interaktive Beispiele besuche: myuninotes-bp.streamlit.app

A) $r_{V D} = 0.25$ da ein schwacher linearer Zusammenhang hervorgeht, dies erkennt man gut an der Regressionslinie

(c) Von drei Messdurchgängen an einer Person wurde einmal vor der Operation, einmal während der Operation und einmal nach der Operation gemessen. Beschreiben Sie anschaulich, wie dies zu Scheinkorrelation führen könnte, wenn, wie oben, die Messungen nicht unterschieden werden. (3 Punkte)

Die Messdurchgänge könnten zu Scheinkorrelation führen, da sie zu jeweiligen Zeitpunkten unter unterschiedlichen Bedingungen stattfinden (z. B. Stress und Fasten vor der Operation, Medikamente währenddessen, Erholung danach). Wenn diese Unterschiede nicht berücksichtigt werden, kann fälschlicherweise ein Zusammenhang zwischen den Messwerten entstehen, obwohl die wahre Ursache die Operationsphasen sind. Durch die Wiederholungsmessungen entsteht eine zeitliche Abhängigkeit, die nicht berücksichtigt wird.

Aufgabe 3 (Bonusaufgabe) (4 Punkte)

In seinem Artikel A Dirty Dozen: Twelve P-Value Misconceptions (2008) beleuchtet Steven Goodman zwölf in der Literatur weit verbreitete Fehlinterpretationen des $p$ -Werts. Erklären Sie in den folgenden Beispielen kurz, worin der Irrtum liegt.

(a) Misconception #1:

“Wenn der $p$ -Wert $P = 0.05$ ist, ist die Nullhypothese nur mit einer Wahrscheinlichkeit von 5% wahr.” (2 Punkte)

Irrtum

Die Aussage verwechselt bedingte Wahrscheinlichkeiten:

Der $p$ -Wert quantifiziert:
$P (Beobachtete Daten (oder extremer) ∣ H_{0} ist wahr)$
→ “Wie extrem sind die Daten unter der Annahme, dass $H_{0}$ gilt?”
Die Fehlinterpretation behauptet fälschlicherweise:
$P (H_{0} ist wahr ∣ Beobachtete Daten)$
→ “Wie wahrscheinlich ist $H_{0}$ angesichts der Daten?”

Korrektur

Der $p$ -Wert ist keine Wahrscheinlichkeit für die Nullhypothese, sondern ein Maß für die Kompatibilität der Daten mit $H_{0}$ .
Beispiel: $p = 0.05$ bedeutet:
“Wenn $H_{0}$ wahr wäre, würde man in 5% aller Studien ein solches (oder extremeres) Ergebnis erhalten – unabhängig davon, ob $H_{0}$ tatsächlich wahr oder falsch ist.”

(b) Misconception #3:

“Ein statistisch signifikantes Ergebnis ist klinisch bedeutend.” (2 Punkte)

Irrtum

Statistische Signifikanz ( $p < α$ ) wird fälschlicherweise mit klinischer Relevanz gleichgesetzt. Dies ignoriert:

Effektstärke:
- Kleine, klinisch irrelevante Effekte (z. B. 1% Risikoreduktion) können bei großer Stichprobe signifikant sein.
- Beispiel: Ein Medikament senkt den Blutdruck um 1 mmHg ( $p = 0.04$ ) → statistisch signifikant, aber klinisch irrelevant.
Kontext:
- Laboreffekte (z. B. Zellkultur) lassen sich nicht direkt auf reale Patientenszenarien übertragen.
False Positives:
- Bei $p = 0.05$ sind 5% aller signifikanten Ergebnisse Zufallstreffer (kein echter Effekt).

Korrektur

Klinische Bedeutsamkeit erfordert:

Praktisch relevante Effektgröße (z. B. “Senkung der Mortalität um 20%”).
Klinische Plausibilität:
- Passt der Effekt zum pathophysiologischen Verständnis?
- Gibt es unerwünschte Nebenwirkungen?
Reproduzierbarkeit:
- Wurde der Effekt in unabhängigen Studien bestätigt?

Fazit

Ein signifikanter $p$ -Wert allein garantiert keine klinische Relevanz. Entscheidend sind Effektgröße, Kontext und Reproduzierbarkeit – nicht nur das Überschreiten eines statistischen Schwellenwerts.

🎓 MyUniNotes

Explorer

EiMedBiom - Beispiel Klausuraufgaben

(a) Interpretieren Sie die drei Odds Ratios. (3 Punkte)

(b) Geben Sie für die Heart Protection Study den Regressionskoeffizienten $β_{1}$ und das zugehörige Konfidenzintervall an. (2 Punkte)

Konfidenzintervall

(c) Erklären Sie, wieso die Odds Ratio in der Beobachtungsstudie und in der randomisierten kontrollierten Studie nicht beide mit dem ersten logistischen Regressionsmodell geschätzt wurden. (2 Punkte)

(d) Welche Alternativen gibt es im Allgemeinen, um für Confounding zu adjustieren? Nennen Sie mindestens drei Alternativen zu einem multiplen Regressionsmodell. (3 Punkte)

(e) Welche Ernährungsempfehlungen würden Sie aufgrund des Ergebnisses der randomisierten klinischen Studie treffen, welche basierend auf den Ergebnissen der Beobachtungsstudie? (2 Punkte)

(f) Was könnten mögliche Gründe für die Diskrepanz zwischen den Ergebnissen der zwei Studien sein? (2 Punkte)

(g) Unter Berücksichtigung der Gründe für die Diskrepanz zwischen den Ergebnissen der randomisierten klinischen Studie und der Beobachtungsstudie, argumentieren Sie ob Vitamin C kardiovaskulären Krankheiten vorbeugen kann. (2 Punkte)

Aufgabe 2 (17 Punkte)

Warum wir $S D (V O_{2 G} - V O_{2 F}) = 43$ verwenden und nicht $S D (V O_{2 G} + V O_{2 F}) = 70$ :

Beispielplot (schematisch)

(b) Welcher der vier Werte entspricht $r_{V D}$ , dem Korrelationskoeffizienten nach Bravais-Pearson von $V O_{2 F}$ und $D O_{2}$ ? Begründen Sie kurz Ihre Entscheidung. (3 Punkte)

(c) Von drei Messdurchgängen an einer Person wurde einmal vor der Operation, einmal während der Operation und einmal nach der Operation gemessen. Beschreiben Sie anschaulich, wie dies zu Scheinkorrelation führen könnte, wenn, wie oben, die Messungen nicht unterschieden werden. (3 Punkte)

Aufgabe 3 (Bonusaufgabe) (4 Punkte)

(a) Misconception #1:

Irrtum

Korrektur

(b) Misconception #3:

Irrtum

Korrektur

Fazit

Graph View

Table of Contents

Backlinks

🎓 MyUniNotes

Explorer

EiMedBiom - Beispiel Klausuraufgaben

(a) Interpretieren Sie die drei Odds Ratios. (3 Punkte)

(b) Geben Sie für die Heart Protection Study den Regressionskoeffizienten β1​ und das zugehörige Konfidenzintervall an. (2 Punkte)

Konfidenzintervall

(c) Erklären Sie, wieso die Odds Ratio in der Beobachtungsstudie und in der randomisierten kontrollierten Studie nicht beide mit dem ersten logistischen Regressionsmodell geschätzt wurden. (2 Punkte)

(d) Welche Alternativen gibt es im Allgemeinen, um für Confounding zu adjustieren? Nennen Sie mindestens drei Alternativen zu einem multiplen Regressionsmodell. (3 Punkte)

(e) Welche Ernährungsempfehlungen würden Sie aufgrund des Ergebnisses der randomisierten klinischen Studie treffen, welche basierend auf den Ergebnissen der Beobachtungsstudie? (2 Punkte)

(f) Was könnten mögliche Gründe für die Diskrepanz zwischen den Ergebnissen der zwei Studien sein? (2 Punkte)

(g) Unter Berücksichtigung der Gründe für die Diskrepanz zwischen den Ergebnissen der randomisierten klinischen Studie und der Beobachtungsstudie, argumentieren Sie ob Vitamin C kardiovaskulären Krankheiten vorbeugen kann. (2 Punkte)

Aufgabe 2 (17 Punkte)

Warum wir SD(VO2G​−VO2F​)=43 verwenden und nicht SD(VO2G​+VO2F​)=70:

Beispielplot (schematisch)

(b) Welcher der vier Werte entspricht rVD​, dem Korrelationskoeffizienten nach Bravais-Pearson von VO2F​ und DO2​? Begründen Sie kurz Ihre Entscheidung. (3 Punkte)

(c) Von drei Messdurchgängen an einer Person wurde einmal vor der Operation, einmal während der Operation und einmal nach der Operation gemessen. Beschreiben Sie anschaulich, wie dies zu Scheinkorrelation führen könnte, wenn, wie oben, die Messungen nicht unterschieden werden. (3 Punkte)

Aufgabe 3 (Bonusaufgabe) (4 Punkte)

(a) Misconception #1:

Irrtum

Korrektur

(b) Misconception #3:

Irrtum

Korrektur

Fazit

Graph View

Table of Contents

Backlinks

(b) Geben Sie für die Heart Protection Study den Regressionskoeffizienten $β_{1}$ und das zugehörige Konfidenzintervall an. (2 Punkte)

Warum wir $S D (V O_{2 G} - V O_{2 F}) = 43$ verwenden und nicht $S D (V O_{2 G} + V O_{2 F}) = 70$ :

(b) Welcher der vier Werte entspricht $r_{V D}$ , dem Korrelationskoeffizienten nach Bravais-Pearson von $V O_{2 F}$ und $D O_{2}$ ? Begründen Sie kurz Ihre Entscheidung. (3 Punkte)