ÜB-8-GnC

Aufgabe 8.1: Backfilling

In dieser Aufgabe befassen Sie sich mit der Job Selection im Resource Scheduling, genauer mit dem Backfilling-Algorithmus.

Grundprinzip des Backfillings

Wie in der Vorlesung besprochen, stellt Backfilling einen Optimierungsmechanismus für Scheduler dar, die verfügbaren Ressourcen besser auszunutzen. Dies geschieht, indem Jobs unter bestimmten Umständen unabhängig von ihrer Warteschlangenreihenfolge ausgeführt werden – zum Beispiel, um frei werdende Ressourcen schon vorher nutzen zu können.

Das Grundprinzip dafür ist einfach: Der Scheduler priorisiert die Jobs in der Warteschlange (Queue) nach bestimmten Faktoren (zum Beispiel der Wartezeit) und ordnet sie anschließend als sortierte „Höchste-Priorität-Zuerst“-Liste neu (oft auch als priorisierte FIFO-Liste bezeichnet). Diese Liste stellt den Schedule dar, der nun ausgeführt wird.

Stößt der Scheduler (in Kooperation mit einem Job Execution Manager) dabei auf einen Job, den er (noch) nicht starten kann, kann er stattdessen Jobs mit niedrigeren Prioritäten starten – vorausgesetzt, diese verzögern die Laufzeit der sich noch in der Warteschlange befindlichen Jobs höherer Priorität nicht. Eine solche Entscheidung hängt von dem dabei verwendeten Reservierungskonzept ab.

• Im konservativen Backfilling erhält jeder Job eine Reservierung (und damit ein festes Ausführungsslot) zugesprochen, sobald er in die Warteschlange eingereiht wird.
• Im aggressiven Backfilling besitzt nur der Warteschlangenkopf eine solche Zusicherung.

Fragen:

1. Welche Grundannahmen liegen dem Backfilling zugrunde bzw. welche Information benötigt der Scheduler im Backfilling?

   Lösung:

   • Der Scheduler benötigt Informationen zu den Ressourcenanforderungen (z. B. Anzahl der Nodes und Walltime), zu den Prioritätskriterien (wie z. B. Wartezeit) und zur Verfügbarkeit der Ressourcen.
   • Es wird angenommen, dass Jobs in einer priorisierten FIFO-Liste verwaltet werden und dass freie Ressourcen genutzt werden, solange dadurch keine Jobs mit höherer Priorität verzögert werden.

2. Nennen Sie Beispiele, warum der Scheduler einen Job möglicherweise nicht starten kann.

   Lösung:

   • Es stehen nicht genügend freie Nodes zur Verfügung.
   • Höher priorisierte Jobs blockieren die benötigten Ressourcen.
   • Beim konservativen Backfilling verhindern vorhandene Reservierungen, dass ein Job früher gestartet wird, da dadurch der Terminierungszeitpunkt bereits reservierter Jobs verschoben würde.

3. Wie kann der Scheduler bestimmen, ob die Ausführung eines Jobs den Terminierungszeitpunkt eines anderen Jobs beeinflusst?

   Lösung:

   • Der Scheduler simuliert den Ablauf des Schedules mit und ohne den zusätzlichen Job.
   • Stellt sich heraus, dass durch das Einfügen des Jobs höher priorisierte Jobs verzögert würden, wird der zusätzliche Job nicht in den Backfill-Plan aufgenommen.

Beispiel

Gegeben seien die Jobs A, B, C, D, E, F, G, H mit den in der folgenden Tabelle angegebenen Jobanforderungen („Minuten“ bezeichnet die geschätzte Reservierungsdauer der Knoten) über die verfügbaren 128 Rechenknoten (Compute Nodes).

Job-ID	Anzahl Nodes	Walltime (in Minuten)	Status
A	32	60	Waiting
B	64	120	Waiting
C	24	180	Waiting
D	50	140	Waiting
E	40	90	Waiting
F	4	50	Waiting
G	4	160	Waiting
H	24	90	Waiting

Gehen Sie nun von der angegebenen Belegung der Job-Queue und einem einfachen Zustandsmodell aus:

• Ist ein Job in die Warteschlange eingereiht worden, befindet er sich im Zustand Ww^{w} (Waiting).
• Ist ein Job zur Ausführung vorgesehen, wechselt er in den Zustand Sd^{d} (Scheduled).
• Wird der Job ausgeführt, befindet er sich im Zustand Rt^{t} (Running).

Gehen Sie weiter davon aus, dass sich zu Beginn alle Jobs in der Queue im Status Ww^{w} (Waiting) befinden und dass die Rechenknoten zuerst „von oben nach unten“ und anschließend „von links nach rechts“ zugeteilt werden.

Fragen zum Beispiel:

4. In welcher Reihenfolge werden die Rechenknoten belegt unter Berücksichtigung der angeforderten Rechenknoten und der geschätzten Reservierungsdauer als Prioritätsmerkmale und unter der Annahme eines konservativen Backfillings?

   Lösung:

   • Beim konservativen Backfilling werden die Jobs nach der kürzesten Walltime priorisiert.
   • Reihenfolge: F (50 min), A (60 min), E (90 min), H (90 min), B (120 min), D (140 min), G (160 min), C (180 min).
   • Belegung der Nodes:
     • F (4 Nodes) → 0–50 Minuten
     • A (32 Nodes) → 0–60 Minuten
     • E (40 Nodes) → 0–90 Minuten
     • H (24 Nodes) → 0–90 Minuten
     • B (64 Nodes) → 90–210 Minuten (nach Freigabe durch A und F)
     • D (50 Nodes) → 90–230 Minuten
     • G (4 Nodes) → 90–250 Minuten
     • C (24 Nodes) → 210–390 Minuten (nach Freigabe durch B)

5. Wie sieht die Queue (jetzt aufgefasst als Prioritätenliste) nach der Belegung aller Rechenknoten aus?

   Lösung:

   • Die Prioritätenliste bleibt sortiert nach Walltime: F, A, E, H, B, D, G, C.
   • Jobs, die bereits einen Ausführungsslot erhalten haben, wechseln in den Zustand Sd^{d} (Scheduled).

6. Welche Jobs können nicht in der Warteschlange „nach vorne wandern“ und warum nicht

   Lösung:

   • Jobs mit sehr langer Walltime (z. B. C und G) oder hohem Ressourcenbedarf (z. B. B und D) können nicht nach vorne rücken, da deren bereits fixierte Reservierungen eine frühere Ausführung verhindern würden.

7. Nehmen Sie nun ein aggressives Backfilling an. In welcher Reihenfolge werden die Rechenknoten nun belegt?

   Lösung:

   • Beim aggressiven Backfilling besitzt nur der Warteschlangenkopf eine feste Reservierung.
   • Jobs mit geringem Ressourcenbedarf können daher früher gestartet werden.
   • Reihenfolge: F, G, H, A, E, B, D, C.

---

Aufgabe 8.2: Der Effekt von Verzögerungen im Backfilling

Gehen Sie von dem Szenario der folgenden Abbildung aus.

In dem Szenario wird in einem 6-Knoten-System Job A auf 4 Knoten mit einer geschätzten Dauer von 3 Stunden ausgeführt. Zwei Jobs befinden sich in der Warteschlange:

• Job B mit einer Anforderung von 5 Knoten über 2 Stunden
• Job C mit einer Anforderung von 2 Knoten über 3 Stunden

Fragen:

8. Warum kann Job B nicht vorher ausgeführt werden?

   Lösung:

   • Job B kann nicht früher starten, da er 5 Knoten benötigt, während zum Backfilling-Zeitpunkt nur 2 Knoten frei sind (aufgrund der Belegung von Job A, der 4 von 6 Knoten in Anspruch nimmt).

9. Nehmen Sie an, Job A beendet seine Ausführung eine Stunde früher (die gestrichelte Linie in der Abbildung). Kann Job B jetzt auch früher starten?**

   Lösung:

   • Auch wenn Job A nun bereits nach 2 Stunden (statt 3) endet und damit 4 Knoten freigibt, reichen diese 4 Knoten nicht aus, um die 5 benötigten Knoten für Job B bereitzustellen.
   • Allerdings könnte Job C (der nur 2 Knoten benötigt) ab der verkürzten Ausführungszeit früher gestartet werden.

---

Aufgabe 8.3: Makespan

In dieser Übung sollen Sie sich mit der makespan-Heuristik auseinandersetzen. Das Problem besteht in der Bereitstellung eines Schedules, so dass der sogenannte makespan optimiert wird (Minimierung der Bearbeitungszeiten (completion time) aller Tasks). Diese Aufgabe besteht deshalb aus drei Teilaufgaben:

10. Wir betrachten zunächst den einfachen Fall des makespan-Schedulings auf identischen Maschinen.
11. Wir erweitern dann für den Grid-/Cloud-Fall.
12. Schließlich kritisieren wir die Verwendbarkeit der makespan-Metrik.

Vorbemerkungen

• Parameter-Sweep-Anwendungen sind Anwendungen, die mehrfach parallel durchgeführt werden, wobei sie identisch sind, jedoch mit unterschiedlichen Parametersätzen. Beispiele finden sich bei Monte-Carlo-Simulationen, Fraktalberechnungen oder Genom-Analysen. Eine Parameter-Sweep-Applikation besteht also aus einer Menge identischer, unabhängiger Tasks, die jeweils auf eigenen Parametersätzen rechnen.
• Zum Zwecke des Schedulings einer Parameter-Sweep-Anwendung auf einem verteilten System kann dieses in erster Näherung als ein heterogenes paralleles Maschinen-System modelliert werden, in dem die Geschwindigkeiten der einzelnen Maschinen unvorhersehbar über die Zeit variieren können. Dabei auftretende Kommunikationslatenzen sind vernachlässigbar.
• Je nach Charakteristik der Anwendungen kann es verschiedene Heuristiken zur Scheduling-Optimierung geben. Ziel ist stets die Minimierung des makespan (auch Produktionsspanne genannt), wobei eine möglichst optimale Nutzung der Betriebsmittel (Ressourcen) angestrebt wird.

---

makespan auf identischen Maschinen

Gegeben sei eine Menge von Jobs $1,\dots ,n$ mit zugeordneten Größen (den Ausführungszeiten) $p_1,\dots ,p_n\in \mathbb{N}$ und eine Menge $1,\dots ,m$ von identischen Maschinen.

Gesucht ist eine Zuteilung $f:[n]\to [m]$ der $n$ Jobs auf die $m$ Maschinen, so dass der makespan

$$\underset{j\in [m]}{\max }\sum _{i\in [n],f(i)=j}{p}_i$$

minimiert wird. Diese Zuteilung wird auch als Schedule bezeichnet.

Für den Fall identischer Maschinen können nun verschiedene Heuristiken für die Zuteilung verwendet werden. Die bekanntesten sind:

• Least-Loaded: Zuteilung der Maschine mit der bisher geringsten Last.
• Longest-Processing-Time (LPT): Sortiere die Prozesse nach ihrer Prozessdauer (längste Prozessdauer zuerst) und weise dann die Maschine mit der bisher geringsten Last zu.

Betrachten Sie nun die folgende Abbildung 7 und die dort dargestellten identischen Maschinen mit ihrer normierten Geschwindigkeit (definiert als die Anzahl der Instruktionen, die in einer Zeiteinheit bearbeitet werden können).

Seien zusätzlich die folgenden Tasklängen gegeben (wieder definiert als die Anzahl der Instruktionen, die abgearbeitet werden müssen):

• Task T₁: 20
• Task T₂: 12
• Task T₃: 17
• Task T₄: 28
• Task T₅: 23

---

Aufgaben:

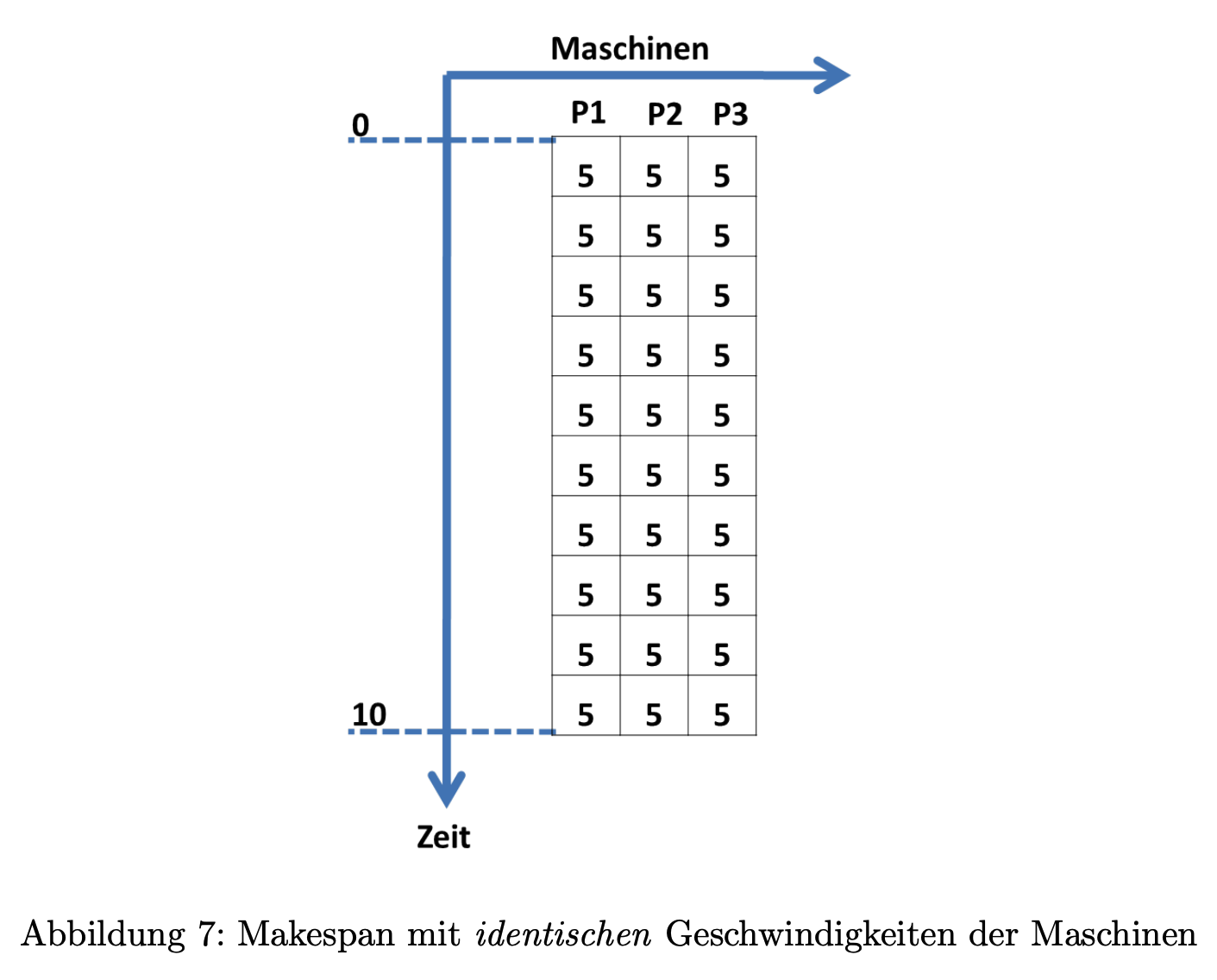
13. Simulieren Sie die Maschinenbelegung nach der Least-Loaded-Heuristik und geben Sie den makespan an.

    Lösung:

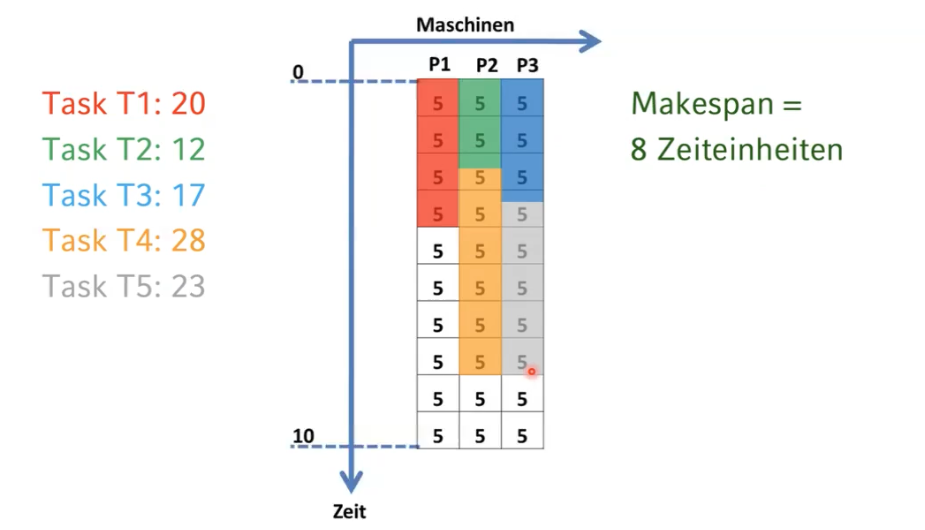
1. Simulieren Sie die Maschinenbelegung nach der Longest-Processing-Time-Heuristik und geben Sie den makespan an.

   Lösung:

---

makespan im Grid

Wie Sie wissen, gelten für Grid-Systeme andere Annahmen, und die Voraussetzungen der vorherigen Übungen müssen revidiert werden. Im Grid können wir auch in diesem abstrakten Modell nicht mehr von identischen Maschinen ausgehen.

Für die weitere Übung betrachten wir deshalb das folgende formale Modell:

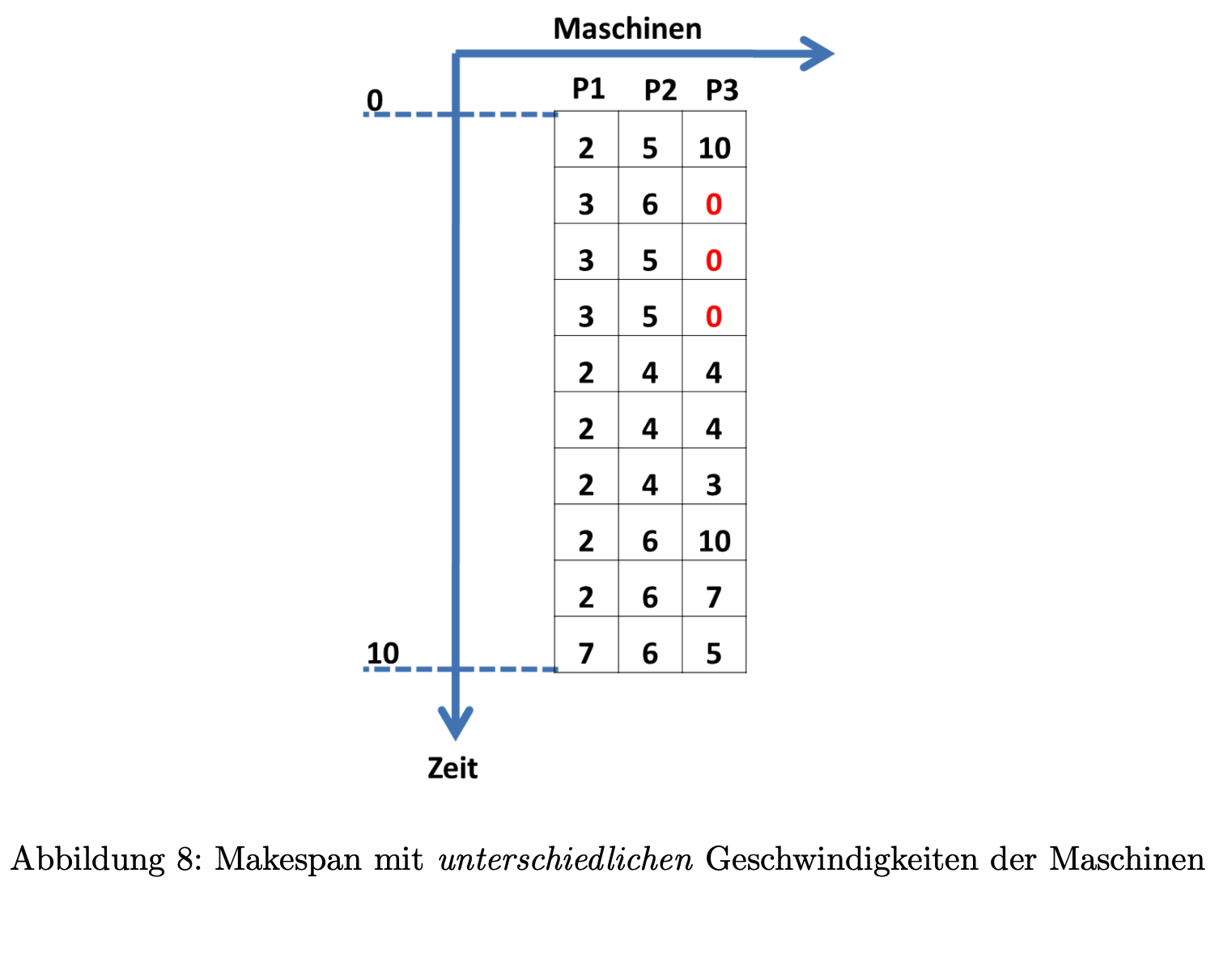
Sei $s_{p,t}$ die Geschwindigkeit der Maschine $p$ im Zeitintervall $[t,t+1]$, wobei $t\in \mathbb{N}$.

OBdA können wir annehmen, dass die Maschinengeschwindigkeit für jedes $t$ im Intervall $[t,t+1]$ konstant ist. Wir nehmen weiter an, dass $s_{p,t}$ a priori unbekannt ist. $s_{p,t}$ kann also auch Null sein (zum Beispiel bei übergroßer Last oder wenn die Maschine abgeschaltet ist).

Der Einfachheit halber sollen das dynamische Hinzufügen und Entfernen von Maschinen sowie Fehlersituationen nicht berücksichtigt werden.

Betrachten Sie nun die folgende Abbildung 8 mit den dort dargestellten Geschwindigkeiten der Maschinen. (Beachten Sie bitte, dass P3 im Intervall $[1,4]$ die Geschwindigkeit 0 besitzt.)

Formales Modell

Sei nun $T$ eine Menge unabhängiger Tasks (gegeben wie zuvor) und sei $m$ die Anzahl der Maschinen (z. B. Ressourcen auf der Fabric-Ebene) im Grid. Dann ist ein Schedule $S$ über $T$ eine endliche Menge von Tripeln $(v,p,t)$ mit:

• $v\in T$ (der Task)
• $1\le p\le m$ (die Maschine)
• $t$ (die Startzeit von $v$)

Ein Tripel $(v,p,t)\in S$ bedeutet:

• Task $v$ wird auf Maschine $p$ im Intervall $[t,t+d]$ ausgeführt.
• $d$ ist so gewählt, dass die auf Maschine $p$ ausgeführten Instruktionen im Intervall $[t,t+d]$ exakt der Tasklänge von $v$ entsprechen.
• $t+d$ ist der Terminierungszeitpunkt von $v$ (completion time).

Randbedingungen

Für jeden Schedule $S$ über $T$ müssen die folgenden Bedingungen erfüllt sein:

2. Jeder Task $v\in T$ muss mindestens einmal ausgeführt werden.
3. Jede Maschine kann zu einem gegebenen Zeitpunkt $t$ nur einen Task $v\in T$ ausführen.

---

Aufgaben:

4. Simulieren Sie die Maschinenbelegung nach der Least-Loaded-Heuristik und geben Sie die genaue Tripel-Sequenz und den makespan an.

   Lösung (Beispielhafte Tripel-Sequenz):

   • Least-Loaded-Heuristik (Grid):

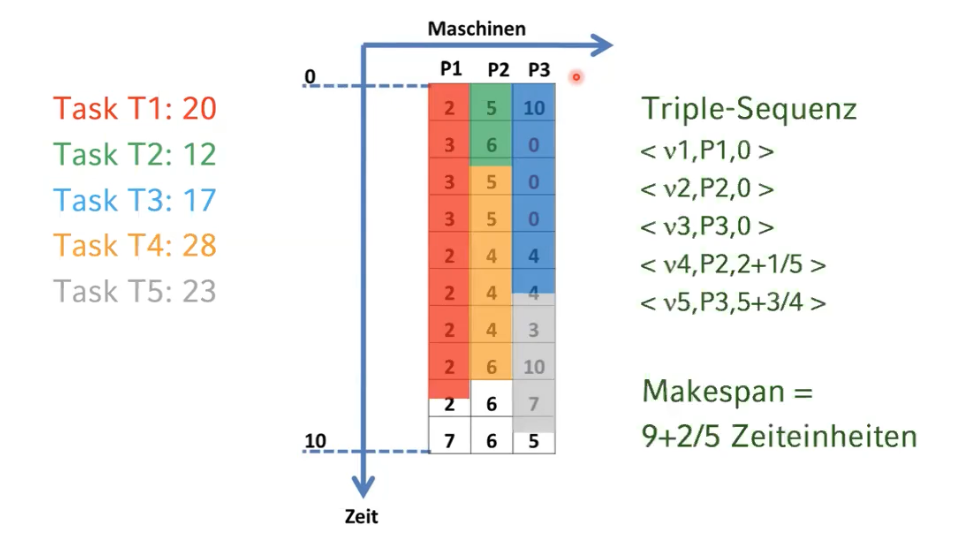
5. Simulieren Sie die Maschinenbelegung nach der Longest-Processing-Time-Heuristik und geben Sie die genaue Tripel-Sequenz und den makespan an.

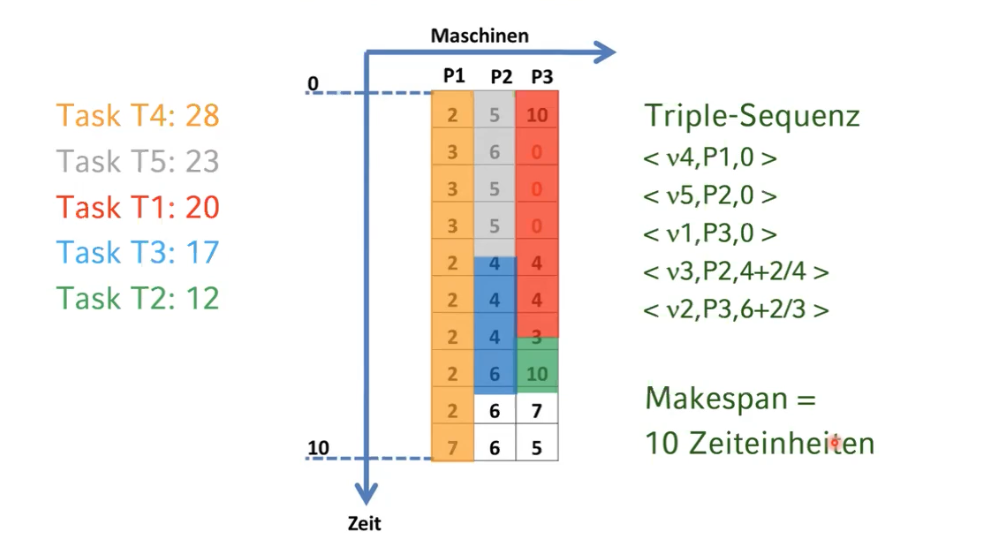
   Lösung (Beispielhafte Tripel-Sequenz):

   • LPT-Heuristik (Grid):

---

Kritik an der makespan-Metrik

Kritisieren Sie bitte die makespan-Metrik in Grids/Clouds auf Grund der Erfahrungen mit den vorherigen Aufgaben. Orientieren Sie sich dabei an den folgenden Fragen:

• Sind die Grundannahmen realistisch?
• Für welche Fälle eignet sich die makespan-Metrik, für welche eher weniger, für welche gar nicht?

Lösung:

• Realitätsnähe:
  Die Annahmen der makespan-Metrik – wie konstante Maschinenleistungen und das Fehlen dynamischer Änderungen – sind in Grid-/Cloud-Umgebungen oft unrealistisch, da diese Systeme durch heterogene Ressourcen und dynamische Laständerungen geprägt sind.
• Eignung:
  • Geeignet: für homogene Umgebungen mit statischen Ressourcen, wo die Maschinenleistungen konstant bleiben.
  • Weniger geeignet: für Grid-/Cloud-Systeme, in denen sich Maschinenleistungen und Auslastungen häufig ändern.
  • Unggeeignet: für Systeme mit Kommunikationsabhängigkeiten oder dynamischer Ressourcenverfügbarkeit, da hier der makespan nicht alle relevanten Aspekte abbildet.

×

MyUniNotes is a free, non-profit project to make education accessible for everyone. If it has helped you, consider giving back! Even a small donation makes a difference.

These are my personal notes. While I strive for accuracy, I’m still a student myself. Thanks for being part of this journey!

---