FSK-1-VL (16.04.2024)

TODO

• 1b und 1c genauer ausarbeiten
• Grammatik 1b wiederholen, vorallem das mit aaaab
• Chomsky-Hierarchie nochmal üben
• Syntaxbäume VL 1c
• Rechts und Linksableitung
• Typen lernen typ1, typ2,typ3
• Entscheidungsprobleme lernen
• Problem vs Sprachen

Geplanter Inhalt dieser VL

• Vorlesung 1a: Begrüßung, Organisatorisches, Inhaltsübersicht und Grundlagen
• Vorlesung 1b: Grammatiken und die Chomsky-Hierarchie
• Vorlesung 1c: Weitere Grammatikbegriffe sowie Eigenschaften von Sprachen

Organisatorisches:

• Zentralübung alle 2 Wochen Mittwochs um 12-14 Uhr in A240
• BONUSPUNKTE!! Immer eine Woche Zeit für (Bonuspunkte wurden abgeschafft aufgrund von rechtlichen Unklarheiten)
• Klausur: 5. August 2024 ab 15:00
• Das Datum der Nachholklausur ist noch nicht bekannt.

Ziel des Moduls

Ziel der Veranstaltung

Das Ziel dieses Moduls ist es, sowohl Theorie also auch Fähigkeiten zu vermitteln:

Theorie

• Was Computer können und was nicht: Die Theorie erklärt, wie schnell und effizient bestimmte Problem durch Computer gelöst werden können und welche Problem außerhalb ihrer Reichweite liegen.
• Praktische Anwendungen: Viele theoretische Konzepte finden Anwendung in der Praxis.
• Ästhetik der Theorie: Theoretische Informatik ist nicht nur nützlich, sondern auch in gewisser Weise ästhetisch ansprechend.

Fähigkeiten

• Umgang mit abstrakten Konzepten: Sie werden lernen, abstrakte Theorien zu verstehen und anzuwenden.
• Sorgfältige und präzise Arbeit: Das Module lehrt Sie, präzise und detailorientiert zu arbeiten.
• Entwicklung von Beweisführungskompetenzen: Sie werden Fähigkeiten entwickeln, um wissenschaftliche Beweise zu führen und zu verstehen.

Inhalte der Veranstaltung

Die theoretische Informatik umfasst drei große Themenbereiche:

1. Formale Sprachen und Automatentheorie

   • Darstellung von Entscheidungsproblemen: Wie können Problem formal und verständlich für Automaten ausgedrückt werden?
   • Erkennung von Programmiersprachen: Methods zur Erkennung und Analyse von Programmiersprachen und anderen formalen Sprachen.

2. Berechenbarkeitstheorie

   • Algorithmische Lösbarkeit: Untersuchung, welche Problem grundsätzlich mit Algorithmen oder Computern gelöst werden können.

3. Komplexitätstheorie

   • Lösbarkeit in annehmbarer Zeit: Erforschung, welche Problem effizient, also in praktisch annehmbarer Zeit, gelöst werden können.

Themen

• Formale Sprachen und Automatentheorie
  • Darstellung von Entscheidungsproblemen
  • Erkennung von Programmiersprachen und ähnlichen Strukturen
  • Schlüsselkonzepte:
    • Formale Sprachen und Entscheidungsprobleme
    • Reguläre Ausdrücke (z.B. für Lexer)
    • Grammatiken (z.B. für Parser)
    • Automaten
• Berechenbarkeitstheorie
  • Welche Problem können algorithmisch gelöst werden?
  • Schlüsselkonzepte:
    • Intuitive Berechenbarkeit
    • Turing-Berechenbarkeit
    • Imperative Programme (LOOP, WHILE, GOTO)
    • Recursive Funktionen
    • Unentscheidbarkeit
• Komplexitätstheorie
  • Welche Problem können in akzeptabler Zeit gelöst werden?
  • Schlüsselkonzepte:
    • Die Klassen $P$ und $NP$
    • $NP$-Schwere, $NP$-Vollständigkeit
    • Konkrete $NP$-vollständige Problem

Vorlesung 1a: Begrüßung, Organisatorisches, Inhaltsübersicht und Grundlagen

Grundlagen: Wörter

Definition DefinitionDefinition

Ein Alphabet $\Sigma$ ist eine endliche nicht leere Menge von Zeichen (oder Symbolen).

Z.B $\Sigma =\{a,b,c,d,e\}$

Definition DefinitionDefinition

Ein Wort w über $\Sigma$ ist eine endliche Folge von Zeichen aus $\Sigma$.

Beispiele:

• bade ist ein Wort über {a,b,c,d,e}
• baden ist kein Wort über {a,b,c,d,e} (n fehlt in Menge)

Weitere Notationen zu Wörtern:

• Das leere Wort wird also $ϵ$ notiert.
• Für $w=a_1\dots a_n$ ist $|w|=n$ die Länge des Wortes.
• Für $1\le i\le |w|$ ist $w[i]$ das Zeichen an der $i$-ten Position in $w$.
• Für $a\in \Sigma$ und $w$ ein Wort über $\Sigma$ sei ${\#}_a(w)\in \mathbb{N}$ die Anzahl an Vorkommen des Zeichens $a$ im Wort $w$.
• Beispiele:
  • Es gilt $|ϵ|=0$ und ${\#}_a(ϵ)=0$ für alle $a\in \Sigma$.
  • Für $\Sigma =\{a,b,c\}$ ist
    • $|abbccc|=6$
    • $|aabbbccc|=8$
    • ${\#}_a(abbccc)=1$
    • ${\#}_c(aabbbccc)=3$.
  • Für $w=abbcd$ ist $w[1]=a$, $w[5]=c$ und $w[7]$ undefiniert.

Konkatenation und Kleene-Stern (REFRACTOR)

Definition DefinitionDefinition

Das Wort $u\cdot v$ (alternativ $uv$) entsteht, indem Wort $v$ hinten an Wort $u$ angehängt wird.

Die Konkatenation hilft folgende Mengen von Wörtern über zu definieren:

Definition DefinitionDefinition

Sei $\Sigma$ ein Alphabet, dann definieren wir:

$$\begin{array}{rl}{\Sigma }^0& :=\{ϵ\}\\ {\Sigma }^i& :=\{aw\mid a\in \Sigma ,w\in {\Sigma }^{i-1}\}\text{ fu¨r }i>0\\ {\Sigma }^{\ast }& :=\bigcup _{i\in \mathbb{N}}{\Sigma }^i\\ {\Sigma }^{+}& :=\bigcup _{i\in {\mathbb{N}}_{>0}}{\Sigma }^i\end{array}$$

Beachte: $\mathbb{N}=\{0,1,2,\dots \}$ und ${\mathbb{N}}_{>0}=\{1,2,\dots \}$.

Beispiele für Konkatenation und Kleene-Stern:

${\Sigma }^0$

• ${\Sigma }^0$ ist definiert also die Menge, die nur das leere Wort $ϵ$ enthält. Da das leere Wort kein Zeichen enthält, ist es das “neutrale Element” der Wortkonkatenation. Für $\Sigma =\{a,b\}$ erhalten wir ${\Sigma }^0=\{ϵ\}$.

${\Sigma }^i$

• ${\Sigma }^i$, für ein gegebenes $i>0$, enthält alle Wörter der Länge $i$. Das bedeutet, dass wir jede Kombination von Zeichen aus $\Sigma$ nehmen und diese zu Wörtern der Länge $i$ zusammensetzen. Zum Beispiel:

  • Für ${\Sigma }^1=\{a,b\}$, weil wir jedes Zeichen aus $\Sigma$ nehmen, das ein Wort der Länge 1 bildet.
  • Für ${\Sigma }^2$ bilden wir alle möglichen Kombinationen von zwei Zeichen: ${\Sigma }^2=\{aa,ab,ba,bb\}$.

${\Sigma }^{\ast }$

• ${\Sigma }^{\ast }$ ist die Kleene-Stern-Operation und umfasst alle Wörter beliebiger Länge, einschließlich des leeren Wortes $ϵ$. Es ist die Vereinigung aller ${\Sigma }^i$ für $i\ge 0$. Für $\Sigma =\{a,b\}$ enthält ${\Sigma }^{\ast }$ also alle möglichen Wörter, die mit ‘a’ und ‘b’ gebildet werden können, wie $\{ϵ,a,b,aa,ab,ba,bb,aaa,\dots \}$.

${\Sigma }^{+}$

• ${\Sigma }^{+}$ ist ähnlich wie ${\Sigma }^{\ast }$, enthält jedoch nicht das leere Wort $ϵ$. Es umfasst alle nicht-leeren Wörter, die aus dem Alphabet $\Sigma$ gebildet werden können. Für $\Sigma =\{a,b\}$ beinhaltet ${\Sigma }^{+}$ die Mengen ${\Sigma }^i$ für alle $i\ge 1$. Das bedeutet, wir haben alle Wörter wie $\{a,b,aa,ab,ba,bb,aaa,\dots \}$, aber nicht $ϵ$.

Beachten Sie, dass beim Übergang von ${\Sigma }^i$ zu ${\Sigma }^{i+1}$, jedes Wort aus ${\Sigma }^i$ mit jedem Zeichen aus $\Sigma$ konkateniert wird, um die Wörter der Länge $i+1$ zu bilden.

Weitere Notationen und Begriffe

Für Wörter über einem Alphabet $\Sigma$ gelten die folgenden Notationen und Begriffe:

• Wenn $w$ ein Wort über $\Sigma$ ist, dann wird durch $w^m$ das Wort bezeichnet, das durch $m$-maliges Konkatenieren von $w$ entsteht, das heißt:
  • $w^0=ϵ$ ist das leere Wort, und für $m>0$ ist $w^m=w{w}^{m-1}$, also das Wort $w$, $m$-mal wiederholt.
• Das rückwärts gelesene Wort von $w$ wird mit $\overline{w}$ bezeichnet. Es gilt also:
  • $\overline{ϵ}=ϵ$ und für $w=a_1{a}_2\dots a_n$ ist $\overline{w}=a_n\dots a_2{a}_1$.
• Ein Wort $w$ ist ein Palindrom, genau dann wenn $w=\overline{w}$, das bedeutet, das Wort ist vorwärts wie rückwärts gelesen gleich.

Beispiele für Palindrome sind:

• “anna"
• "reliefpfeiler"
• "lagerregal"
• "annasusanna”

Palindrome sind in der theoretischen Informatik ein interessanter Fall, weil sie oft in der Automatentheorie zur Demonstration der Eigenschaften von speziellen Automaten oder zur Illustration von Grenzen bestimmter Arten von Automaten verwendet werden.

Sprechweisen: Präfix, Suffix, Teilwort

Seien $u,v$ Wörter über einem Alphabet $\Sigma$.

• $u$ ist ein Präfix von $v$, wenn es ein Wort $w$ gibt mit $uw=v$.
• $u$ ist ein Suffix von $v$, wenn es ein Wort $w$ gibt mit $wu=v$.
• $u$ ist ein Teilwort von $v$, wenn es Wörter $w_1,w_2$ gibt mit $w_{1}u{w}_2=v$. $⟹$ Präfix und Suffix impliziert Teilwort!

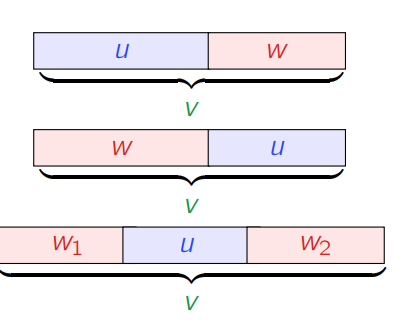
Beispiel: Sei $w=ababbaba$.

• $w$ ist ein Präfix, Suffix und Teilwort von $w$.
• $aba$ ist ein Präfix, Suffix und Teilwort von $w$.
• $ababb$ ist ein Präfix und Teilwort von $w$, aber kein Suffix von $w$.
• $bab$ ist ein Teilwort von $w$, aber weder ein Präfix noch ein Suffix.
• 
  
• w ist ein Präfix, Suffix und Teilwort von w.
• aba ist ein Präfix, Suffix und Teilwort von w. (WARUM TEILWORT??) !!! $⟹$ Präfix und Suffix impliziert Teilwort!
• ababb ist ein Präfix und Teilwort von w, aber kein Suffix von w.
• bab ist ein Teilwort von w, aber weder ein Präfix noch ein Suffix.
• 
  
• Das ganze Wort ababbaba ist ein Präfix, Suffix und Teilwort von w.
• ababbaba ist ein Präfix, Suffix und Teilwort von w, gefunden am Anfang, am End und in der Mitte des Wortes.
• ababbaba ist ein Präfix und Teilwort von w, gefunden am Anfang und in der Mitte des Wortes, aber kein Suffix.
• abababbaba ist ein Teilwort von w, gefunden in der Mitte des Wortes, aber weder ein Präfix noch ein Suffix.

Grundlagen: Formale Sprache

Formale Sprachen sind ein grundlegendes Konzept in der Informatik und der theoretischen Computerwissenschaft, das zur Beschreibung und Analyse von Syntax und strukturellen Mustern von Daten und Anweisungen verwendet wird. Sie bestehen aus Alphabeten, die die Grundbausteine der Sprachen sind, und Regeln, die definieren, wie Zeichen zu gültigen Strings oder „Wörtern“ kombiniert werden können. Diese Sprachen werden oft verwendet, um die Syntax von Programmiersprachen zu definieren, aber auch in der Automatentheorie, der Komplexitätstheorie und der Logik.

Definition DefinitionDefinition

Eine (formale) Sprache $L$ über dem Alphabet $\Sigma$ ist eine Teilmenge von ${\Sigma }^{\ast }$ d.h $L\subseteq {\Sigma }^{\ast }$ Kann leeres Wort enthalten z.B kann eine Textdatei leer sein

Beachte: L steht für “Language”

Definition DefinitionDefinition

Seien $L$, $L_1$, $L_2$ formale Sprachen über dem Alphabet $\Sigma$. Dann sind folgende Operationen definiert:

• Vereinigung:
  • Die Vereinigung von $L_1$ und $L_2$ ist definiert also
  • $L_1\cup L_2=\{w|w\in L_1$ oder $w\in L_2\}$
• Schnitt:
  • Der Schnitt von $L_1$ und $L_2$ ist definiert also
  • $L_1\cap L_2=\{w|w\in L_1$ und $w\in L_2\}$
• Komplement:
  • Das Komplement zu $L$ ist definiert also
  • $\overline{L}={\Sigma }^{\ast }\setminus L$
• Product:
  • Das Product von $L_1$ und $L_2$ ist definiert also
  • $L_1\cdot L_2=L_1{L}_2=\{uv|u\in L_1$ und $v\in L_2\}$

Eine (formale) Sprache $L$ über dem Alphabet $\Sigma$ ist eine Teilmenge von ${\Sigma }^{\ast }$, d.h. $L\subseteq {\Sigma }^{\ast }$.

Beispiel

Beispiele für Operationen auf formalen Sprachen

Gegeben sei das Alphabet $\Sigma =\{a,b\}$ und zwei formale Sprachen $L_1=\{a^i|i\in \mathbb{N}\}$ und $L_2=\{b^i|i\in \mathbb{N}\}$.

• $L_1\cup L_2$ ist die Sprache der Wörter, die nur aus $a$‘s oder nur aus $b$‘s bestehen. $ϵ$ ist inkludiert da epsilon a und auch b ist
• $L_1\cap L_2=\{\epsilon \}$, wobei $\epsilon$ das leere Wort darstellt und zeigt, dass beide Sprachen das leere Wort enthalten. $\{\epsilon \}\ne \varnothing$
• $\overline{L_1}$ ist die Sprache der Wörter, die mindestens ein $b$ enthalten.
• $L_1{L}_2=\{a^i{b}^j|i,j\in \mathbb{N}\}$ ist die Sprache, die aus allen Kombinationen von $a$‘s gefolgt von $b$‘s besteht.
• $L_2{L}_1=\{b^i{a}^j|i,j\in \mathbb{N}\}$ ist die Sprache, die aus allen Kombinationen von $b$‘s gefolgt von $a$‘s besteht.
• $L_1{L}_1=L_1$ zeigt, dass die Konkatenation von $L_1$ mit sich selbst die Sprache nicht verändert.

Kleenescher Abschluss

Sei $L$ eine Sprache. Dann ist der Kleenesche Abschluss von $L$, benannt nach Stephen Cole Kleene, definiert also:

$$\begin{array}{rlrl}{L}^0& :=\{ϵ\}& L^{\ast }& :=\bigcup _{i\in \mathbb{N}}{L}^i\\ L^i& :=L\cdot L^{i-1}\text{ fu¨r }i>0& L^{+}& :=\bigcup _{i\in {\mathbb{N}}_{>0}}{L}^i\end{array}$$

Beispiel

Z.B L = Englisch dann L^5 fünf englische Wörter

Gegeben sei die Sprache $L=\{ab,ac\}$.

$$L^0=\{ϵ\}$$

Das bedeutet, $L^0$ ist die Sprache, die nur das leere Wort $ϵ$ enthält. Dies ist in der Definition des Kleeneschen Abschlusses enthalten und repräsentiert die $0$-fache Konkatenation von Wörtern aus $L$, also kein Wort.

$$L^1=L\cdot L^0=L=\{ab,ac\}$$

$L^1$ ist gleich $L$, da die einmalige Konkatenation eines Wortes aus $L$ mit dem leeren Wort $ϵ$ das ursprüngliche Wort ergibt. Deshalb ist $L^1$ die Sprache $L$ selbst.

$$L^2=L\cdot L^1=\{abab,abac,acab,acac\}$$

$L^2$ entspricht der zweifachen Konkatenation der Wörter aus $L$. Jedes Wort aus $L$ wird mit jedem Wort aus $L$ kombiniert, was die Sprache $L^2$ ergibt, die aus allen möglichen Kombinationen von zwei Wörtern aus $L$ besteht.

$$L^3=L\cdot L^2=\{ababab,ababac,abacab,abacac,acabab,acabac,acacab,acacac\}$$

Analog dazu ist $L^3$ die dreifache Konkatenation der Wörter aus $L$. Jedes Wort aus $L^2$ wird mit jedem Wort aus $L$ kombiniert. Dadurch entstehen längere Wörter, die aus drei Segmenten bestehen, die jeweils aus $L$ stammen.

In diesen Beispielen zeigt sich, dass mit steigendem $i$, $L^i$ eine Sprache darstellt, die aus Wörtern besteht, die durch $i$-fache Konkatenation der Wörter aus $L$ gebildet werden. Der Kleenesche Abschluss $L^{\ast }$ umfasst dann alle diese Möglichkeiten einschließlich des leeren Wortes.

Weitere Beispiele für Operationen auf formalen Sprachen

Im Kontext formaler Sprachen können komplexe Strukturen wie Zeitangaben oder Zahlenreihen durch die Verknüpfung einfacherer Sprachen konstruiert werden. Hier sind zwei Beispiele dafür:

• Die Sprache aller gültigen Uhrzeiten lässt sich ausdrücken also:

  $$((\{ϵ,1\}\cdot \{0,\dots ,9\})\cup (\{2\}\cdot \{0,1,2,3\}))\cdot \{:\}\cdot (\{0,1,2,3,4,5\}\cdot \{0,\dots ,9\})$$

  Diese Sprache beschreibt die Kombination von Stunden und Minuten, wobei Stunden von 00 bis 23 und Minuten von 00 bis 59 abgedeckt werden. Das Zeichen $\{:\}$ steht dabei also Trennzeichen zwischen Stunden und Minuten.

• Die Sprache aller natürlichen Zahlen kann repräsentiert werden durch:

  $$\{0\}\cup (\{1,\dots ,9\}\cdot \{0,\dots ,9{\}}^{\ast })$$

  Hierbei beschreibt der erste Teil $\{0\}$ die Zahl Null, und der zweite Teil die natürlichen Zahlen beginnend mit einer Ziffer von 1 bis 9, gefolgt von beliebig vielen Ziffern von 0 bis 9, was allen natürlichen Zahlen außer der Null entspricht.

---

Vorlesung 1b: Grammatiken und die Chomsky-Hierarchie

Grundlagen der Grammatiken

Grammatiken ermöglichen die Definition formaler Sprachen, die aus Wörtern bestehen, welche gemäß spezifischer Regeln gebildet werden.

Definition einer Grammatik

Definition

Eine Grammatik $G$ ist definiert also ein 4-Tupel $(V,\Sigma ,P,S)$, wobei:

• $V$ eine endliche Menge von Variable ist, auch Nichtterminale genannt.
• $\Sigma$ ein Alphabet von Terminalsymbolen ist, das disjunkt zu $V$ ist ($V\cap \Sigma =\varnothing$).
• $P$ eine endliche Menge von Produktionsregeln ist, wobei jede Regel eine Form $\ell \to r$ hat.
• $S\in V$ das Startsymbol ist.

Beispiel

Grammatik für einfache arithmetische Ausdrücke:

• $V=\{\text{E},\text{T},\text{F}\}$
• $\Sigma =\{+,\ast ,(,),\text{id}\}$
• $P$ enthält Regeln wie:
  • $\text{E}\to \text{E}+\text{T}|\text{T}$
  • $\text{T}\to \text{T}\ast \text{F}|\text{F}$
  • $\text{F}\to (\text{E})|\text{id}$
• $S=\text{E}$

Syntaxbäume

Syntaxbäume visualisieren, wie Sätze aus der Grammatik abgeleitet werden können, und illustrieren die Anwendung von Produktionsregeln in einer hierarchischen Struktur.

Chomsky-Hierarchie

Die Chomsky-Hierarchie klassifiziert Grammatiken nach der Komplexität ihrer Produktionsregeln.

Definition

• Typ 0 (Rekursiv aufzählbar): Keine Einschränkungen für die Produktionsregeln.
• Typ 1 (Kontextsensitiv): Alle Regeln $\ell \to r$ erfüllen $|\ell |\le |r|$, was bedeutet, dass die Länge der linken Seite kleiner oder gleich der rechten Seite ist.
• Typ 2 (Kontextfrei): Jede Regel ist von der Form $A\to \gamma$, mit $A\in V$ und $\gamma \in (V\cup \Sigma {)}^{\ast }$.
• Typ 3 (Regulär): Regeln sind von der Form $A\to aB$ oder $A\to a$, mit $A,B\in V$ und $a\in \Sigma$.

Beispiele für Grammatiken in der Chomsky-Hierarchie

Reguläre Grammatiken erzeugen einfache Sprachen, typisch für viele Textverarbeitungsaufgaben:

• Grammatik für das Erkennen von Kennworten mit Buchstaben gefolgt von Zahlen.

Weitere Begriffe und Definitionen

Definition

• Satzform: Ein Wort über $(V\cup \Sigma {)}^{\ast }$, das durch das Startsymbol $S$ beginnt und durch Anwenden von Regeln aus $P$ abgeleitet wird.
• Ableitung: Ein Process, bei dem durch Anwenden von Produktionsregeln aus einer Satzform schrittweise Wörter über ${\Sigma }^{\ast }$ erzeugt werden.
• Linksableitung: Eine Ableitung, bei der immer das linkeste Nichtterminal ersetzt wird.

Abschluss und Weiterführende Themen

Die nächste Vorlesung behandelt spezielle Typen von Grammatiken und ihre Anwendung in der Analyse und Erzeugung von Programmiersprachen. Weitere Themen umfassen die Entscheidbarkeitstheorie und die Automatentheorie, die in der theoretischen Informatik von zentraler Bedeutung sind.

---

Vorlesung 1c: Weitere Grammatikbegriffe sowie Eigenschaften von Sprachen

Wiederholung: Definition einer Grammatik

Note

Eine Grammatik $G$ ist ein 4-Tupel $(V,\Sigma ,P,S)$, wobei:

• $V$ eine endliche Menge von Variable (alternativ Nichtterminalen) ist,
• $\Sigma$ ein Alphabet von Zeichen (alternativ Terminalen) ist, das disjunkt zu $V$ ist $(V\cap \Sigma =\varnothing )$,
• $P$ eine endliche Menge von Produktionsregeln ist, von der Form $\ell \to r$ mit $\ell \in (V\cup \Sigma {)}^{+}$ und $r\in (V\cup \Sigma {)}^{\ast }$,
• $S\in V$ das Startsymbol (alternativ Startvariable) ist.

Die Chomsky-Hierarchie

Note

• Typ 0 (Rekursiv aufzählbar): Keine Einschränkungen für die Produktionsregeln.
• Typ 1 (Kontextsensitiv): Für alle $\ell \to r\in P$ ist $|\ell |\le |r|$.
• Typ 2 (Kontextfrei): $\ell \to r\in P$ wobei $\ell \in V$.
• Typ 3 (Regulär): Für alle $A\to r\in P$ gilt $r=a$ oder $r=a{A}^{\prime }$ für $a\in \Sigma$ und $A^{\prime }\in V$, d.h. die rechten Seiten sind Wörter aus $\Sigma \cup \Sigma V$.

Syntaxbäume

Note

Der Syntaxbaum zeigt, wie ein Wort durch Anwendung der Produktionsregeln einer Grammatik generiert wird. Die Wurzel des Baumes ist das Startsymbol $S$, und die Blätter sind die Terminale, die das Wort bilden. Die innere Struktur des Baumes repräsentiert die Anwendung der Produktionsregeln.

Beispiel eines Syntaxbaums

Die Grammatik $G=(\{E,M,Z\},\{+,\ast ,(,),1,2\},P,E)$ mit Regeln wie $E\to E+M$ und $M\to M\ast Z$ kann den Ausdruck $1\ast 2$ mit unterschiedlichen Ableitungen darstellen, die jedoch denselben Syntaxbaum nutzen:

    E
   / \
  M   M
 /     \
1       2

Links- und Rechtsableitungen

Links- und Rechtsableitungen beschreiben, wie das linkeste oder rechteste Nichtterminal in einer Satzform schrittweise ersetzt wird, um ein Wort in der Sprache zu generieren.

Beispiel für Linksableitung

E
⇒ E + M
⇒ M + M
⇒ M * Z + M
⇒ 1 * Z + M
⇒ 1 * 2 + M
⇒ 1 * 2 + Z
⇒ 1 * 2 + 3

Erweiterte Backus-Naur-Form (EBNF)

Note

EBNF ist eine Notation für kontextfreie Grammatiken, die es erlaubt, Regeln kompakter auszudrücken:

• Alternativen: $A\to w_1|w_2|\dots |w_n$
• Optionale Elemente: $A\to u[v]w$
• Wiederholungen: $A\to u\{v\}w$

Anwendungen von kontextfreien Grammatiken

Kontextfreie Grammatiken werden häufig zur syntaktischen Analyse in der Programmierung verwendet. Tools wie YACC, ANTLR und PLY nutzen diese Grammatiken, um Parser für verschiedene Programmiersprachen zu generieren. Diese Werkzeuge transformieren grammatikbasierte Spezifikationen direkt in den Quellcode von Parsern, die dann in der Softwareentwicklung eingesetzt werden können.

Beispiel: ANTLR Grammatik

Ein typisches ANTLR Grammatikbeispiel sieht wie folgt aus:

prog: (expr NEWLINE)*;

expr: expr (’*’ | ’/’) expr | expr (’+’ | ’-’) expr | INT | ’(’ expr ’)‘;

Diese Definition erlaubt die Erkennung und syntaktische Analyse von einfachen mathematischen Ausdrücken.

Abgeschlossenheit von Sprachen

Die Abgeschlossenheit einer Sprachklasse bezieht sich darauf, ob die Klasse under bestimmten Operationen wie Vereinigung, Schnitt, Komplement und Produktbildung geschlossen ist. Das heißt, das Ergebnis der Operation fällt immer noch in dieselbe Klasse.

Entscheidbarkeit und Problem

Bestimmte Eigenschaften wie Entscheidbarkeit sind zentral für das Verständnis der Berechenbarkeitstheorie. Eine Sprache ist entscheidbar, wenn es möglich ist, mit einem endlichen Verfahren (Algorithmus) zu bestimmen, ob ein beliebiges Wort zur Sprache gehört.

> Entscheidbarkeit: Eine Sprache ist entscheidbar, wenn es einen Algorithmus gibt, der in endlicher Zeit entscheidet, ob ein gegebenes Wort zur Sprache gehört oder nicht.

Zusammenfassung der Chomsky-Hierarchie

Die Chomsky-Hierarchie ordnet Sprachen basierend auf ihren grammatikalischen Einschränkungen in vier Typen. Diese Hierarchy hilft nicht nur, die theoretischen Grundlagen der Sprachverarbeitung zu verstehen, sondern auch praktische Parsing-Strategien zu entwickeln.

---