Bayes-Prinzip

Prinzip

In den letzten beiden Kapiteln haben wir einfache Anwendungen der Bayes-Formel kennen gelernt. Wir erweitern diese Anwendung nun auf allgemeinere stochastische Modelle. Um daraus Schlüsse zu ziehen, verwenden wir das Bayes-Prinzip

Bayes-Prinzip

Bayesianische Inferenz

Im Folgenden wiederholen und verallgemeinern wir das Vorgehen in unseren bisherigen Beispielen:

• Wir beobachten $n$ Daten $x_i$, die aus einem Zufallsprozess entstanden sind.
• Die $x_i$ sind Realisierungen einer Zufallsvariable $X_i$.
• $X_i$ hat eine Verteilung mit (Daten-)Dichte (Likelihood) $f(x)$.
• Wir kennen die Datendichte aber nicht vollständig, sondern nur bis auf Parameter $\theta$: $f(x|\theta )$
• $\theta$ ist unbekannt und die Information über $\theta$ lässt sich in Form einer Dichte darstellen
• Vor der Beobachtung (a priori) ist unsere Information ausgedrückt durch die Priori-Dichte $p(\theta )$
• Durch Beobachtung erhalten wir mehr Information, ausgedrückt durch die a posteriori-Dichte $p(\theta |x)$

Bisher waren $x$ und $\theta$ eindimensional, im Folgenden können sie aber auch mehrdimensional sein!

Aufgaben in der Bayesianischen Inferenz

• Festlegung des statistischen Modells für $x$ und damit der Datendichte (Likelihood) $f(x|\theta )$
• Festlegung des a priori-Wissens über $\theta$, also der Priori-Dichte $p(\theta )$
• Berechnung der Posteriori $p(\theta |x)$

Bayes-Prinzip

• Die Dichte der Posteriori-Verteilung erhalten wir über die Bayes-Formel: $$p(\theta |x)=\frac{f(x|\theta )\cdot f(\theta )}{\int f(x|{\theta }^{\prime })f({\theta }^{\prime })d{\theta }^{\prime }}$$

Bayes-Prinzip Alle Schlüsse werden nur aus der Posteriori-Verteilung gezogen.

• Die Posteriori enthält alle Informationen über $\theta$ nach der Beobachtung.
• Umso mehr Informationen die Daten über $\theta$ enthalten, umso weniger unsicher sind wir über $\theta$: Die Varianz der Posterioriverteilung ist kleiner, die Dichtefunktion konzentriert sich in einem (oder mehreren) Bereichen.

Was machen wir mit der Posteriori?

• Grundsätzlich gilt: Die komplette Posteriori ist wichtig. Wenn möglich, sollten wir diese komplett darstellen – bei hochdimensionalen Parametern $\theta =({\theta }_1,\dots ,{\theta }_p)$ ist dies aber schwierig. Hier bietet es sich an, jeden Parameter einzeln anzuschauen; genauer: die marginale Posteriori von ${\theta }_i|x$ zu betrachten.

Aus der Posteriori können wir dann folgende Schlüsse ziehen:

• Punktschätzer: (wir kennen den Posterior-Erwartungswert, außerdem gibt es den Maximum-a-Posteriori-Schätzer/Posteriori-Modus und den Posteriori-Median)
• Intervallschätzer
• Tests
• Modellvergleich
• Prädiktion

Zusammenfassung

Zusammenfassung des Bayes-Prinzips

Bayesianische Inferenz

Bayesianische Inferenz ist ein Ansatz in der Statistik, bei dem Wissen über eine unbekannte Größe (Parameter $\theta$) durch beobachtete Daten verbessert wird. Dies geschieht durch den Einsatz von Wahrscheinlichkeitsmodellen, die wie folgt definiert sind:

• Es werden $n$ Datenpunkte $x_i$ beobachtet, die aus einem Zufallsprozess stammen und Realisierungen einer Zufallsvariable $X_i$ sind.
• Jede $X_i$ folgt einer Verteilung, deren Form durch die Parameter $\theta$ bestimmt wird: $f(x|\theta )$.
• Vor der Datenerhebung besteht eine anfängliche Einschätzung des Parameters $\theta$, ausgedrückt durch die Priori-Dichte $p(\theta )$.
• Nach der Datenerhebung wird diese Einschätzung durch die Posteriori-Dichte $p(\theta |x)$ aktualisiert, welche mittels der Bayes-Formel berechnet wird: $$p(\theta |x)=\frac{f(x|\theta )\cdot p(\theta )}{\int f(x|{\theta }^{\prime })p({\theta }^{\prime })d{\theta }^{\prime }}$$

Aufgaben und Verwendung der Posteriori

• Statistisches Modell festlegen: Auswahl von $f(x|\theta )$ und $p(\theta )$.
• Posteriori berechnen: Diese enthält alle Informationen über $\theta$ nach dem Einbezug der Daten und wird für alle weiteren Schlüsse verwendet.
• Analyse der Posteriori: Bei mehrdimensionalen $\theta$ betrachtet man oft die marginale Posteriori jedes Parameters ${\theta }_i|x$.

Anwendungen der Posteriori

Aus der Posteriori lassen sich verschiedene statistische Schlüsse ziehen, darunter:

• Punktschätzer: Berechnung des Erwartungswertes, des Maximum-a-Posteriori-Schätzers und des Medians.
• Intervallschätzer: Bestimmung von Konfidenzintervallen.
• Tests: Durchführung statistischer Hypothesentests.
• Modellvergleich: Vergleich unterschiedlicher statistischer Modelle.
• Prädiktion: Vorhersage zukünftiger Beobachtungen basierend auf dem Modell.

Zusammengefasst ermöglicht das Bayes-Prinzip eine systematische Aktualisierung des Wissens über einen Parameter durch die Kombination von Priori-Information und Daten, wobei die Posteriori-Dichte als Grundlage für alle weiteren statistischen Analysen dient.

---

Prioris

Ein wichtiger Baustein der Bayes-Inferenz ist die Wahl der Prioris. Schauen wir uns Möglichkeiten zur Wahl der Priori an und kommen dazu zurück zum

Beta-Binomial-Modell

Lernziele

• Konstruktion konjugierter Prioris
• Anwendung und Kritik subjektiver Prioris
• Konstruktion einfacher nicht-informativer Prioris

Konjugierte Prioris

Wir hatten im Beispiel mit den Billardkugeln festgestellt, dass die Kombination von Binomialverteilung der Daten und Gleichverteilung als Priori gut zusammen passt: Wir erhalten eine bekannte Verteilung als Posteriori.

Allgemein definieren wir: Eine Familie $\mathcal{F}$ von Verteilungen auf $\Theta$ heißt konjugiert, zu einer Dichte $f(x|\theta )$, wenn für jede Priori $p(\theta )$ auf $\mathcal{F}$ die Posteriori $p(\theta |x)$ ebenfalls zu $F$ gehört

Vereinfacht Gesagt

Konjugierte Prioris sind spezielle Priori-Verteilungen in der Bayesianischen Statistik, die die Berechnung der Posteriori-Verteilung vereinfachen. Wenn eine Priori-Verteilung konjugiert zur Likelihood-Funktion der Daten ist, bleibt die Form der Posteriori-Verteilung innerhalb derselben Familie von Verteilungen. Das bedeutet, dass sowohl die Priori als auch die Posteriori den gleichen Typ von Verteilung aufweisen, was die Analyse und Berechnungen einfacher macht.

Beispiel nach Bayes

Im Beispiel der Billardkugeln hatten wir die Gleichverteilung als Spezialfall der Betaverteilung als Priori und die Betaverteilung als Posteriori.

• Anzahl der Kugeln rechts von der weißen Kugel: $X\sim B(n,\pi )$
• Priori-Annahme für $\pi$: $\pi \sim Beta(a,b)$ mit $a=b=1$

Wir nennen dieses Modell Beta-Binomial-Modell (Beta-Priori und Binomial-Datenmodell). Im Folgenden benutzen wir ganz allgemein die Parameter $a$ und $b$ in der Beta-Priori und werden dann auch andere Werte für die Priori-Parameter zulassen.

Man erkennt die Konjugiertheit am ähnlichen Aufbau von Datendichte (eine Funktion in $x$) und Priori, bezogen auf den unbekannten Parameter $\pi$ (wir betrachten hier nur jeweils den Kern der Dichte, lassen also Konstanten weg):

$$f(x|\pi )\propto {\pi }^x(1-\pi {)}^{n-x}$$ $$p(\pi )\propto {\pi }^{a-1}(1-\pi {)}^{b-1}$$

Zusammen also:

$$p(\pi |x)\propto f(x|\pi )p(\pi )\propto {\pi }^{x+a-1}(1-\pi {)}^{n-x+b-1}$$

Posteriori-Parameter

• Die Posteriori-Verteilung von $\pi |x$ ist also eine Beta$(\hat{a},\hat{b})$-Verteilung mit $\hat{a}=x+a$ und $\hat{b}=n-x+b$. Die Parameter der Posterioriverteilung, also die Posteriori-Parameter setzen sich jeweils aus Informationen der Priori und der Datendichte zusammen.
• Allgemein fasst die Posteriori Informationen aus der Priori und der Datendichte zusammen.
• Hier ist $\hat{a}$ die Summe der Priori-Parameter $a$ und der Anzahl an Erfolgen $x$. Entsprechend ist $\hat{b}$ die Summe des Priori-Parameters $b$ und der Anzahl an Misserfolgen $n-x$.

Rückschluss auf die Priori-Parameter

• Das heißt also, wenn wir $a$ um eins erhöhen, ergibt sich für die Posteriori das selbe Ergebnis, wie wenn man die Anzahl der Erfolge um eins erhöht.
• $a$ kann also in gewisser Weise auch die Priori-Anzahl an Erfolgen interpretiert werden, entsprechend ist $b$ die Priori-Anzahl an Misserfolgen.

Vereinfacht Gesagt

Das Konzept der konjugierten Prioris ist ein zentrales Element in der Bayesianischen Statistik, das insbesondere die Berechnung der Posteriori-Verteilung vereinfacht. Konjugierte Prioris sind speziell ausgewählte Priori-Verteilungen, die dazu führen, dass die Posteriori-Dichte der gleichen Verteilungsfamilie angehört wie die Priori-Dichte. Dies bedeutet, dass wenn eine Priori-Verteilung konjugiert zur Likelihood-Funktion der Daten ist, die resultierende Posteriori-Verteilung denselben Typ von Verteilung aufweist wie die Priori, was mathematische Berechnungen und statistische Analysen erleichtert.

Beispiel: Das Beta-Binomial-Modell

In einem anschaulichen Beispiel mit Billardkugeln nutzen wir eine Betaverteilung als Priori und eine Binomialverteilung als Modell für die Daten. Dieses Zusammenwirken wird als Beta-Binomial-Modell bezeichnet:

• Nehmen wir an, die Anzahl der Kugeln rechts von einer weißen Kugel folgt einer Binomialverteilung $X\sim B(n,\pi )$.
• Die Priori-Annahme für die Wahrscheinlichkeit $\pi$, dass eine Kugel rechts von der weißen Kugel liegt, wird als Betaverteilung modelliert: $\pi \sim Beta(a,b)$, wobei wir zunächst $a=b=1$ setzen, was einer Gleichverteilung entspricht.

Die Binomialverteilung für die Daten und die Betaverteilung für die Priori sind konjugiert, was mathematisch bedeutet:

• Die Likelihood-Funktion hat die Form $f(x|\pi )\propto {\pi }^x(1-\pi {)}^{n-x}$.
• Die Priori-Dichte wird als $p(\pi )\propto {\pi }^{a-1}(1-\pi {)}^{b-1}$ angenommen.
• Multiplizieren wir diese beiden, erhalten wir die Posteriori-Dichte: $p(\pi |x)\propto {\pi }^{x+a-1}(1-\pi {)}^{n-x+b-1}$.

Schlussfolgerungen aus der Posteriori

Die Posteriori-Verteilung nach Beobachtung der Daten ist wieder eine Betaverteilung, Beta$(\hat{a},\hat{b})$, mit den neuen Parametern:

• $\hat{a}=x+a$ (Summe aus der Anzahl der Erfolge und dem Priori-Parameter $a$)
• $\hat{b}=n-x+b$ (Summe aus der Anzahl der Misserfolge und dem Priori-Parameter $b$)

Diese Parameteraktualisierung zeigt, wie Informationen aus der Priori-Verteilung (unsere Vorannahmen) und der Likelihood (Informationen aus den neuen Daten) in der Posteriori-Verteilung kombiniert werden. Die Priori-Parameter $a$ und $b$ können dabei als hypothetische Anzahl an Erfolgen bzw. Misserfolgen vor den neuen Beobachtungen interpretiert werden. Diese Interpretation erleichtert das Verständnis dafür, wie Vorwissen und neue Daten in der Bayesianischen Analyse zusammenfließen.

Quiz zu konjugierten Prioris

Sei $X$ Erlang-verteilt mit unbekanntem Parameter $\lambda$ und bekanntem $n$. Die Erlang-Verteilung ergibt sich zum Beispiel als Summe von unabhängigen Wartezeiten. Die Dichte der Erlang$(n,\lambda )$-Verteilung ist:

$$f(x)=\frac{1}{(n-1)!}{\lambda }^n{x}^{n-1}\exp (-\lambda x)$$

Info

Die Erlang-Verteilung wird verwendet, um die Verteilung von Wartezeiten zu beschreiben, wenn mehrere Ereignisse eintreten müssen. Sie ist eine Verallgemeinerung der Exponentialverteilung, bei der $n$ unabhängige Ereignisse mit der gleichen Rate $\lambda$ eintreten müssen, bevor das beobachtete Ereignis auftritt.

Was ist die konjugierte Priori-Verteilung für \lambda?

• Gamma-Verteilung mit $p(\lambda )\propto {\lambda }^{a-1}\exp (-b\lambda )$
• Exponential-Verteilung mit $p(\lambda )\propto \exp (-\lambda )$
• Beta-Verteilung mit $p(\lambda )\propto {\lambda }^{a-1}(1-\lambda {)}^{b-1}$

  Lösung p(\lambda) \propto \lambda^{a-1} \exp(-b\lambda)

  Erklärung: Die Gamma-Verteilung ist die konjugierte Priori-Verteilung für den Parameter $\lambda$ einer Erlang-Verteilung, da ihre Form ermöglicht, dass die Posteriori-Verteilung wieder eine Gamma-Verteilung ist, was die Berechnungen vereinfacht.

Sei $X\sim Erlang(n,\lambda )$-verteilt und die Priori-Verteilung $\lambda \sim Ga(a,b)$

Wie ist die Posteriori-Verteilung von \lambda|x?

• Ga$(a+x,b+n)$
• Erlang$(a+n-1,b+x)$
• Ga$(a+n,b+x)$
• Ga$(a+n-1,b+x)$

  Lösung (a+n, b+x)

  Erklärung: Bei der Erlang-Verteilung von $X$ mit $X\sim \text{Erlang}(n,\lambda )$ und der Priori-Verteilung $\lambda \sim \text{Ga}(a,b)$ summiert sich der Parameter $a$ der Gamma-Priori um $n$ (weil $n$ Ereignisse zur Likelihood beitragen) und der Parameter $b$ um $x$ (die beobachtete Summe der Wartezeiten), um die Posteriori-Parameter $\hat{a}=a+n$ und $\hat{b}=b+x$ zu bilden. Dies stellt die natürliche Aktualisierung im Rahmen der Bayes’schen Statistik dar und behält die Form der Gamma-Verteilung bei, was Rechnungen vereinfacht.

Erlang-Verteilung und die Posteriori

Erlang-Verteilung und ihre Posteriori-Analyse

Die Erlang-Verteilung ist eine spezielle Form der Gamma-Verteilung und wird oft verwendet, um die Summe von mehreren unabhängigen, identisch exponentialverteilten Wartezeiten zu beschreiben. Diese wird insbesondere in der Warteschlangentheorie und Zuverlässigkeitstechnik angewendet. Die Erlang-Verteilung ist definiert durch zwei Parameter: die Form $n$, welche die Anzahl der Ereignisse angibt, und die Rate $\lambda$, welche die Rate dieser Ereignisse darstellt.

Mathematische Definition

Die Dichte der Erlang-Verteilung, Erlang$(n,\lambda )$, ist gegeben durch:

$$f(x)=\frac{1}{(n-1)!}{\lambda }^n{x}^{n-1}{e}^{-\lambda x}$$

Hierbei ist $x$ die Summe der Wartezeiten, und der Parameter $n$ muss eine ganze Zahl sein.

Bayesianische Analyse

Wenn $X$ erlang-verteilt mit bekannten $n$ und unbekanntem $\lambda$ ist und $\lambda$ eine Gamma-Priori-Verteilung $\text{Ga}(a,b)$ hat, ergibt die bayesianische Analyse eine Posteriori-Verteilung für $\lambda$, die auch eine Gamma-Verteilung ist.

Posteriori-Verteilung

Die Parameter der Posteriori-Verteilung $\text{Ga}(a^{\prime },b^{\prime })$ werden aktualisiert zu:

$$a^{\prime }=a+n,b^{\prime }=b+x$$

• $a^{\prime }$ (Formparameter): Erhöht um die Anzahl der Ereignisse $n$, da jedes Ereignis als “Erfolg” im Sinne des Bayes’schen Lernens zählt.
• $b^{\prime }$ (Ratenparameter): Erhöht um die beobachtete Summe der Wartezeiten $x$, da $\lambda$ in der Erlang-Verteilung die Rate dieser Wartezeiten darstellt und eine höhere Summe der Wartezeiten eine höhere Rate impliziert, die für die Berechnung der neuen Erwartung von $\lambda$ benötigt wird.

Fazit

Diese Analyse ist zentral für Anwendungen, wo die Verteilung von Wartezeiten in Prozessen (wie Telekommunikationsnetzwerken oder Fertigungsstraßen) modelliert werden muss und wo Parameter unsicher sind und aus Daten gelernt werden sollen.

Informative und subjektive Priori

Wir können also in die Priori-Verteilung “Information reinstrecken”. Und zwar theoretisch beliebig viel!

Zu viel Priori-Information

Nehmen wir im Billard-Beispiel als Priori $\pi \sim \text{Beta}(100,100)$ und rollen dann zehn rote Kugeln, die alle links von der weißen Kugel zum Liegen kommen. Die Posteriori ist dann $\pi \sim \text{Beta}(110,100)$ und die Posteriori-Dichte sieht so aus:

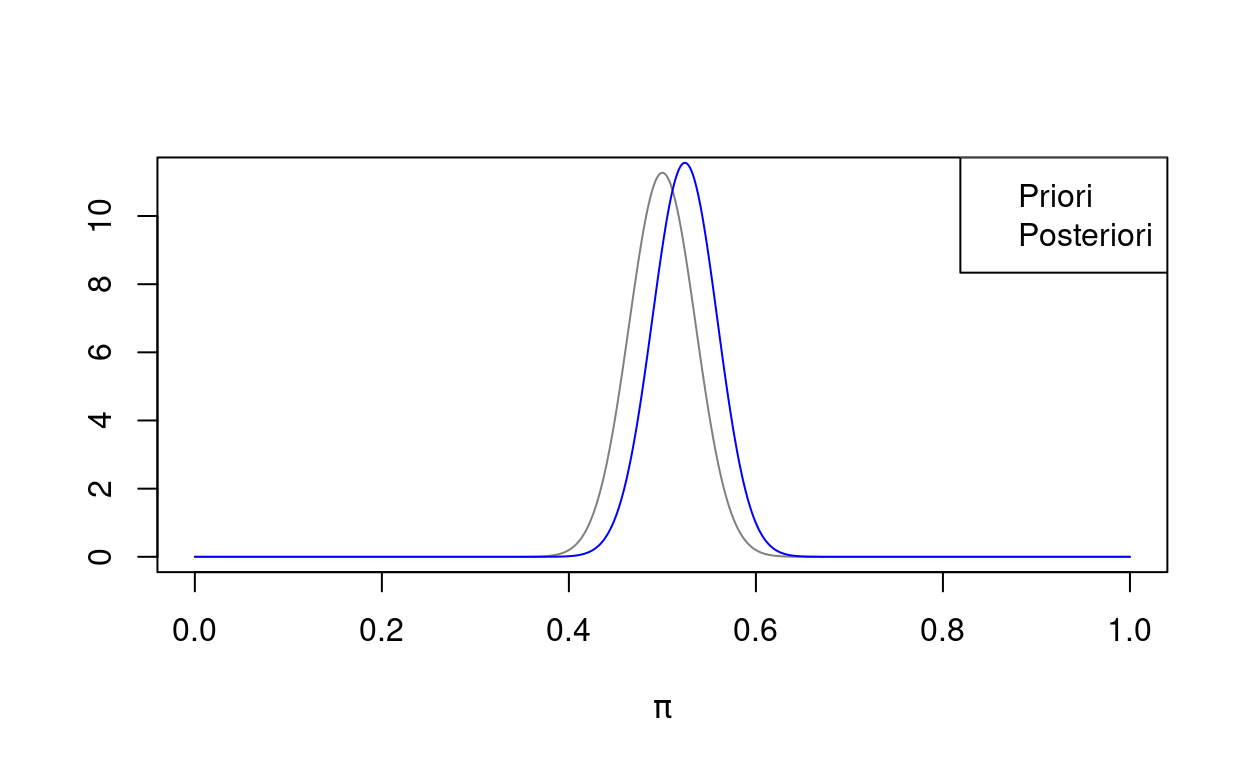
Die Posteriori unterscheidet sich auch kaum von der Priori, obwohl die Daten darauf hindeuten, dass die weiße Kugel weit rechts liegt.

Kritik an der Bayes-Inferenz

Die Möglichkeit, mit der Priori die Posteriori – und damit das Ergebnis – weitgehend festzulegen, ist traditionell ein großer Kritikpunkt an der Bayes-Inferenz. Eine derartige Vorfestlegung des Ergebnisses entspricht natürlich nicht wissenschaftlichen Grundsätzen.

Als Ausweg daraus kann man nicht informative Priors verwenden. Dafür werden wir uns den Begriff der Information noch genauer ansehen müssen.

Ein weiterer Anwendungsbereich der Bayes-Statistik liegt aber genau in der Nutzung von Vorwissen. Dieses kann zum Beispiel aus vorherigen Beobachtungen stammen – wir sprechen von sequentiellem Lernen, siehe dazu das Frosch-Beispiel – oder aus anderen Quellen, z.B. Expertenwissen.

Ein dritter Ansatzpunkt ist, die Priors als Teil der Modellierung zu verwenden. Zum Beispiel in dem man Parameter absichtlich Richtung Null drückt oder Abhängigkeiten zwischen Parametern berücksichtigt. Insbesondere in hochdimensionalen, eventuell überparametrisierten Modellen ist dies hilfreich. Dazu später mehr.

Nichtinformativen Priori

Im Beispiel der Billardkugeln hatten wir die Priori-Parameter $a$ und $b$ als Priori-Erfolge bzw. Priori-Misserfolge interpretiert. Intuitiv heißt keine Information, dass $a=0$ und $b=0$.

Priori ohne Vorinformation

Setzen wir $a=0$ und $b=0$ in den Kern der Beta-Verteilung ein, erhalten wir die sogenannte Haldane-Priori:

$$p(\pi )\propto {\pi }^{-1}(1-\pi {)}^{-1}$$

Form der Haldane-Priori

Der Verlauf dieser Dichte, wie unten dargestellt, zeigt deutlich die Singularitäten an den Rändern bei 0 und 1.

Allerdings existiert das Integral ${\int }_0^1{\pi }^{-1}(1-\pi {)}^{-1}d\pi =\infty$, was zeigt, dass es keine echte Dichtefunktion ist, da das Integral einer Dichte immer 1 sein muss.

Die Haldane-Priori kann man herleiten als Grenzfall einer Beta$(a,b)$-Verteilung mit $a\to 0$ und $b\to 0$.

Uneigentliche Verteilungen

Das die Haldane-Priori keine Dichte hat, ist aber (erstmal) kein Problem! Wir verwenden diese uneigentliche Verteilung trotzdem.

Allgemein definieren wir eine uneigentliche oder impropere Verteilung mit Dichte $f(\theta )$ wie folgt:

• $f(\theta )\ge 0$ für alle $\theta$ (wie bei jeder Dichte)
• $\int f(\theta )d\theta =\infty$ (“eigentlich” müsste das Integral gleich 1 sein)

Posteriori bei uneigentlicher Verteilung

Im Billard-Beispiel haben wir $\pi \sim \text{Beta}(0,0)$ - die Verteilung setzen wir hier in Anführungszeichen, denn die Priori ist eigentlich keine Beta-Verteilung. Trotzdem entspricht sie von der Form her der konjugierten Priori. Es gilt also für die Posteriori in diesem Fall:

$$p(\pi |x)\propto p(\pi )\cdot f(x|\pi )={\pi }^{-1}(1-\pi {)}^{-1}\cdot {\pi }^x(1-\pi {)}^{n-x}={\pi }^{x-1}(1-\pi {)}^{n-x-1}$$

Dies entspricht der Dichte einer Beta$(x,n-x)$-Verteilung, wenn $x>0$ und $n-x>0$, also wenn wir mindestens einen Erfolg und mindestens einen Misserfolg beobachtet haben.

Implikationen

• Aus einer uneigentlichen Posterioriverteilung können wir keine Schlüsse ziehen: weder können wir eine Posterioriwahrscheinlichkeit berechnen noch einen Posteriori-Erwartungswert.
• Die uneigentliche Priori führt aber im Regelfall zu einer eigentlichen oder properen Posterioriverteilung, aus der wir Schlüsse ziehen können.
• Nur in Ausnahmefällen kann eine uneigentliche Posterioriverteilung resultieren – dies muss man im Einzelfall überprüfen.

Laplace-Priori

---