Limo-Klausur-SS23

---

Inhaltsverzeichnis

Aufgabe 1

(a) Modellgleichung und Modellannahmen

• Stellen Sie anhand des R-Outputs die Modellgleichung zu Modell 1.1 auf.
• Welche Modellannahmen werden bezüglich der Störterme getroffen?

(b) Interpretation der Koeffizienten

• Interpretieren Sie die geschätzten Koeffizienten der Variablen Geschl und KrankNacht.

(c) Vergleich von Regressionsmodellen

• Erläutern Sie für Modell 1.2 und Modell 1.3 das jeweilige Vorgehen bei der Modellierung der Kovariable KrankNacht.
• Vergleichen Sie Modell 1.2 und Modell 1.3 mit Modell 1.1 im Hinblick auf die Modellgüte und die erhaltenen Koeffizienten bezüglich der Anzahl der Nächte, die im Krankenhaus verbracht wurden.
• Beschreiben Sie eine Möglichkeit, wie der Zusammenhang zwischen den Variablen KrankNacht und LebenZuf flexibler modelliert werden könnte.

(d) Interpretation der ANOVA-Ergebnisse

• Interpretieren Sie anhand des R-Outputs das Ergebnis der durchgeführten ANOVA bezüglich der Variable BeziehStat.

Aufgabe 2

(a) Interpretation des Intercepts

• Interpretieren Sie den geschätzten Intercept.

(b) Effektplot erstellen

• Zeichnen Sie in das vorgegebene Diagramm einen Effektplot mit den gemäß Modell 2.1 erwarteten Schnabellängen für die drei Pinguinarten für beide Geschlechter ein.

(c) Hypothesentest zur Pinguinart

• Geben Sie die Hypothesen für den linearen Hypothesentest der Form (A\beta = c) an.
• Geben Sie die Matrizen (A) und (c) sowie die Verteilung der Teststatistik an.

(d) Interpretation der Teststatistiken und p-Werte

• Erklären Sie, was bei dem Test bezüglich des Koeffizienten zur Pinguinart Chinstrap inhaltlich überprüft wird.

(e) Annahmen im Modell 2.1

• Welche implizite Annahme wurde in Modell 2.1 bezüglich des Effektes der Pinguinart getroffen?
• Erklären Sie anhand des R-Outputs, ob diese Annahme gerechtfertigt ist.

(f) Effektkodierung in Modell 2.1

• Geben Sie die Koeffizienten (\beta*{0,eff}), (\beta*{1,eff}), (\beta*{2,eff}) und (\beta*{3,eff}) an, die man bei einer Effektkodierung erhalten würde.

Aufgabe 3

(a) Struktur- und Verteilungsannahme

• Geben Sie anhand des R-Outputs zu Modell 3.1 die Struktur- und Verteilungsannahme des Modells an.
• Spezifizieren Sie den linearen Prädiktor.

(b) Interpretation der Koeffizienten auf Ebene der Odds

• Interpretieren Sie die geschätzten Koeffizienten der Variablen ehejahre und kinder auf Ebene der Odds.

(c) Modellierung der Interaktionseffekte

(i) Linearer Prädiktor für Modell 3.2

• Geben Sie den linearen Prädiktor für Modell 3.2 an.

(ii) Vergleich des Risikos für außereheliche Affären

• Vergleichen Sie das Risiko für mindestens eine außereheliche Affäre zwischen einer seit sieben Jahren verheirateten 30-jährigen Frau mit und ohne Kinder.

(iii) Wahrscheinlichkeit für außereheliche Affären bei Männern

• Vergleichen Sie die Wahrscheinlichkeit für mindestens eine außereheliche Affäre bei einem 30-jährigen Mann, der seit 10 Jahren verheiratet ist, je nach Kinderstatus.

Aufgabe 4

(a) Modell 4.1: Beurteilung der Modellgüte

(i) Beurteilung der Modellgüte

• Beurteilen Sie die Modellgüte von Modell 4.1 anhand des Modelloutputs.

(ii) Notwendigkeit der Variablenselektion

• Begründen Sie, warum eine Variablenselektion sinnvoll sein könnte.

(iii) Vergleich der Modelle anhand von AIC

• Vergleichen Sie Modell 4.1 und Modell 4.2 anhand der AIC-Werte.

(d) Variablenselektionsprozesse

• Begründen Sie, warum ein schrittweiser Variablenselektionsprozess vorteilhaft sein könnte.

(e) Problematik der p-Wert-basierten Variablenselektion

• Erläutern Sie, warum es problematisch ist, eine Variablenselektion anhand von p-Werten durchzuführen.

Aufgabe 5

(a) Unterschied zwischen partiellen und sequentiellen Quadratsummen

• Erklären Sie den Unterschied zwischen partiellen und sequentiellen Quadratsummen am Beispiel eines Regressionsmodells.

(b) Problematik bei paarweisen Hypothesentests

• Erläutern Sie die Problematik bei paarweisen Hypothesentests zwischen allen Fachrichtungen und beschreiben Sie eine mögliche Strategie zur Lösung.

(c) Unterschied zwischen einflussreichen Beobachtungen und Ausreißern

• Erklären Sie den Unterschied zwischen einflussreichen Beobachtungen und Ausreißern bei einem linearen Regressionsmodell.

(d) Modellierung wiederholter Messungen

(i) Verletzung der Modellannahmen und Lösung

• Beschreiben Sie, welche Modellannahme verletzt ist und wie diese Problematik behoben werden kann.

(ii) Umgang mit unterschiedlichen Residualstreuungen

• Diskutieren Sie, ob das Modell aus der vorherigen Teilaufgabe noch geeignet ist, wenn die Streuung der Residuen für die einzelnen ProbandInnen unterschiedlich groß ist.

---

Aufgabe 1

Aufgabenstellung

Im Rahmen des Sozio-ökonomischen Panels werden u.a. auch Informationen zur Lebenszufriedenheit der teilnehmenden Personen erhoben. Die TeilnehmerInnen beantworten hierzu die Frage, wie zufrieden Sie gegenwärtig mit ihrem Leben seien, auf einer Skala von 0 bis 10, wobei höhere Werte eine höhere Lebenszufriedenheit entsprechen.

In dieser Aufgabe werden die Daten aus dem Jahr 2017 verwendet, um die Lebenszufriedenheit anhand mehrerer Kovariablen zu den gegenwärtigen Lebensumständen der TeilnehmerInnen zu modellieren.

Für die Analyse werden die folgenden Variablen verwendet:

Variable	Beschreibung
LebenZuf	Lebenszufriedenheit (0 = sehr unzufrieden, 10 = vollkommen zufrieden)
Geschl	Geschlecht (m = männlich, w = weiblich)
KrankNacht	Anzahl der Nächte, die im letzten Jahr im Krankenhaus verbracht wurden
OB5	Persönlichkeitsmerkmal Offenheit (0 = gering, 7 = sehr hoch)
BeziehStat	Beziehungsstatus (Unterscheidung in sieben Kategorien)

Im Folgenden ist der R-Output eines Regressionsmodells zur Beschreibung der Lebenszufriedenheit (Modell 1.1) gegeben:

Modell 1.1

mod1 <- lm(LebenZuf ~ Geschl + KrankNacht + OB5, data = soep17)
summary(mod1)

Call:
lm(formula = LebenZuf ~ Geschl + KrankNacht + OB5, data = soep17)
 
Residuals:
     Min       1Q   Median       3Q      Max
-7.8112  -0.6479   0.4118   0.9315   7.6434
 
Coefficients:
            Estimate Std. Error t value Pr(>|t|)
(Intercept)  6.58028    0.059585 109.223  <2e-16 ***
GeschlW     -0.018981   0.028594  -0.664  0.507
KrankNacht  -0.029844   0.001972 -15.135  <2e-16 ***
OB5          0.193141   0.012164  15.879  <2e-16 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
 
Residual standard error: 1.628 on 13111 degrees of freedom
Multiple R-squared:  0.03566,    Adjusted R-squared:  0.03544
F-statistic: 161.6 on 3 and 13111 DF,  p-value: < 2.2e-16

(a) Stellen Sie anhand des R-Outputs die Modellgleichung zu Modell 1.1 auf. Welche Modellannahmen werden bezüglich der Störterme getroffen? (6 Punkte)

Strukturannahmen: ${ϵ}_i$ ist $N(0,{\sigma }^2)$ für $i=1,\dots ,n$. Störterme folgen einer Normalverteilung mit einem Mittelwert von 0.

$$\text{Lebenszufriedenheit}={\beta }_0+{\beta }_1\text{Geschlecht}+{\beta }_2\text{KrankNacht}+{\beta }_3\text{OB5}+{ϵ}_i$$

Bewertung: 5/6 Punkten

$$\text{LebenZuf}=6.58028-0.018981\cdot \text{GeschlW}-0.029844\cdot \text{KrankNacht}+0.193141\cdot \text{OB5}+ϵ$$

LebenZuf = 6.58028 - 0.018981 * GeschlW - 0.029844 * KrankNacht + 0.193141 * OB5
			+ ε

Modellannahmen bezüglich der Störterme

1. Lineare Beziehung: Die Beziehung zwischen den Prädiktoren und der Zielvariable ist linear.
2. Unabhängigkeit: Die Residuen sind unabhängig.
3. Homoskedastizität: Die Varianz der Residuen ist konstant.
4. Normalverteilung: Die Residuen sind normalverteilt mit Mittelwert 0.

Diese Annahmen sind notwendig für valide Schätzungen und Inferenz im linearen Regressionsmodell.

(b) Interpretieren Sie die geschätzten Koeffizienten der Variablen Geschl und KrankNacht. (5 Punkte)

• Geschl (Geschlecht)

  • Koeffizient: (-0.018981)
  • Interpretation: Wenn das Geschlecht von männlich (0) auf weiblich (1) wechselt, verringert sich die Lebenszufriedenheit im Durchschnitt um 0.018981 Einheiten. Dieser Effekt ist jedoch statistisch nicht signifikant $(p=0.507)$.

• KrankNacht (Anzahl der Nächte im Krankenhaus)

  • Koeffizient: (-0.029844)
  • Interpretation: Jede zusätzliche Nacht im Krankenhaus im letzten Jahr ist mit einer durchschnittlichen Abnahme der Lebenszufriedenheit um 0.029844 Einheiten verbunden. Dieser Effekt ist statistisch signifikant $(p<2e-16)$.

(c) In der Analyse werden nun zwei Regressionsmodelle (Modell 1.2 und Modell 1.3) betrachtet, bei denen im Vergleich zu Modell 1.1 die Kovariable KrankNacht auf alternative Weise in die Modellierung eingeflossen ist. Dabei ergeben sich die folgenden R-Outputs:

Modell 1.2

soep17$Log_Krank <- log10(soep17$KrankNacht + 1)
mod1_2 <- lm(LebenZuf ~ Geschl + Log_Krank + OB5, data = soep17)
summary(mod1_2)

Call:
lm(formula = LebenZuf ~ Geschl + Log_Krank + OB5, data = soep17)
 
Residuals:
     Min       1Q   Median       3Q      Max
-7.7523  -0.6421   0.3740   1.0165   4.3148
 
Coefficients:
            Estimate Std. Error t value Pr(>|t|)
(Intercept)  6.56862    0.05967 110.072  <2e-16 ***
GeschlW     -0.016156   0.02852  -0.566  0.571
Log_Krank   -0.39516    0.02527 -15.646  <2e-16 ***
OB5          0.189504   0.01213  15.615  <2e-16 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
 
Residual standard error: 1.624 on 13111 degrees of freedom
Multiple R-squared:  0.04032,    Adjusted R-squared:  0.04010
F-statistic: 184.7 on 3 and 13111 DF,  p-value: < 2.2e-16

Modell 1.3

soep17$Krank <- ifelse(KrankNacht >= 1, TRUE, FALSE)
mod1_3 <- lm(LebenZuf ~ Geschl + Krank + OB5, data = soep17)
summary(mod3)

Call:
lm(formula = LebenZuf ~ Geschl + Krank + OB5, data = soep17)
 
Residuals:
     Min       1Q   Median       3Q      Max
-7.7415  -0.6305   0.3853   1.0192   3.7532
 
Coefficients:
            Estimate Std. Error t value Pr(>|t|)
(Intercept)  6.55285    0.06001 109.201  <2e-16 ***
GeschlW     -0.01579    0.02865  -0.551  0.582
KrankTRUE   -0.55961    0.04205 -13.310  <2e-16 ***
OB5          0.19017    0.01210  15.599  <2e-16 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
 
Residual standard error: 1.631 on 13111 degrees of freedom
Multiple R-squared:  0.03189,    Adjusted R-squared:  0.03167
F-statistic: 144 on 3 and 13111 DF,  p-value: < 2.2e-16

(i) Erklären Sie für Modell 1.2 und Modell 1.3 kurz das jeweilige Vorgehen bei der Modellierung der Kovariable KrankNacht. (4 Punkte)

• Modell 1.2:

  • Vorgehen: Die Kovariable KrankNacht wurde logarithmisch transformiert. Dies bedeutet, dass der natürliche Logarithmus von $(\text{KrankNacht}+1)$ als Prädiktor verwendet wird.
  • Ziel: Die logarithmische Transformation wird angewendet, um die Skalenverzerrung zu reduzieren und die Verteilung der Nächte im Krankenhaus zu normalisieren.
  • Formel: $$\text{Log\_Krank}={\log }_{10}(\text{KrankNacht}+1)$$

• Modell 1.3:

  • Vorgehen: Die Kovariable KrankNacht wurde in eine binäre Variable umgewandelt. Diese Variable ist TRUE, wenn $\text{KrankNacht}\ge 1$, und FALSE, wenn $\text{KrankNacht}=0$.
  • Ziel: Die binäre Umwandlung ermöglicht die Unterscheidung zwischen Personen, die mindestens eine Nacht im Krankenhaus verbracht haben, und denen, die keine Nacht im Krankenhaus verbracht haben.
  • Formel: $$\text{Krank}=\text{ifelse}(\text{KrankNacht}\ge 1,\text{TRUE},\text{FALSE})$$

(ii) Vergleichen Sie Modell 1.2 und Modell 1.3 mit Modell 1.1 im Hinblick auf die Modellgüte und die erhaltenen Koeffizienten bezüglich der Anzahl der Nächte, die im Krankenhaus verbracht wurden. (4 Punkte)

Modellgüte

• Modell 1.1:

  • Multiple R-squared: 0.03566
  • Adjusted R-squared: 0.03544
  • Residual standard error: 1.628
  • F-statistic: 161.6 on 3 and 13111 DF, p-value: < 2.2e-16

• Modell 1.2:

  • Multiple R-squared: 0.04032
  • Adjusted R-squared: 0.04010
  • Residual standard error: 1.624
  • F-statistic: 184.7 on 3 and 13111 DF, p-value: < 2.2e-16

• Modell 1.3:

  • Multiple R-squared: 0.03189
  • Adjusted R-squared: 0.03167
  • Residual standard error: 1.631
  • F-statistic: 144 on 3 and 13111 DF, p-value: < 2.2e-16

Vergleich der Modellgüte

• Modell 1.2 hat die höchste Modellgüte, wie durch den höheren Multiple und Adjusted R-squared im Vergleich zu Modell 1.1 und Modell 1.3 ersichtlich.
• Modell 1.3 hat die niedrigste Modellgüte, wie durch den niedrigeren Multiple und Adjusted R-squared im Vergleich zu Modell 1.1 und Modell 1.2 ersichtlich.

Vergleich der Koeffizienten

• Modell 1.1:

  • $\text{KrankNacht}$: $-0.029844$ (p-value: < 2e-16)

• Modell 1.2:

  • $\text{Log\_Krank}$: $-0.39516$ (p-value: < 2e-16)

• Modell 1.3:

  • $\text{KrankTRUE}$: $-0.55961$ (p-value: < 2e-16)

Interpretation der Koeffizienten

• In Modell 1.1 reduziert jede zusätzliche Nacht im Krankenhaus die Lebenszufriedenheit um etwa $0.029844$ Einheiten.
• In Modell 1.2 reduziert ein Anstieg des logarithmierten Werts der Nächte im Krankenhaus um eine Einheit die Lebenszufriedenheit um etwa $0.39516$ Einheiten.
• In Modell 1.3 reduziert das Verbringen von mindestens einer Nacht im Krankenhaus die Lebenszufriedenheit um etwa $0.55961$ Einheiten im Vergleich zu keiner Nacht im Krankenhaus.

Zusammenfassend zeigt Modell 1.2 die beste Anpassung an die Daten, gefolgt von Modell 1.1, während Modell 1.3 die geringste Modellgüte aufweist. Die negativen Koeffizienten in allen Modellen deuten darauf hin, dass mehr Nächte im Krankenhaus (oder die Anwesenheit im Krankenhaus überhaupt) mit einer geringeren Lebenszufriedenheit verbunden sind.

(iii) Beschreiben Sie eine Möglichkeit, wie der Zusammenhang zwischen den Variablen KrankNacht und LebenZuf flexibler modelliert werden könnte. (2 Punkte)

Es gibt mehrere Möglichkeiten, den Zusammenhang zwischen KrankNacht und LebenZuf flexibler zu modellieren:

1. Polynomialer Regressionsansatz:

   • Durch Hinzufügen von höheren Potenzen der Variablen KrankNacht kann eine nichtlineare Beziehung modelliert werden: $$\text{LebenZuf}={\beta }_0+{\beta }_1\cdot \text{KrankNacht}+{\beta }_2\cdot {\text{KrankNacht}}^2+{\beta }_3\cdot {\text{KrankNacht}}^3+ϵ$$ Dies erlaubt es, die Kurvenform der Beziehung zwischen KrankNacht und LebenZuf besser zu erfassen.

2. Splines:

   • Durch die Verwendung von Splines (wie natürliche Splines oder B-Splines) können verschiedene Segmente der Daten unterschiedlich angepasst werden, was zu einer flexibleren Modellierung führt: $$\text{LebenZuf}={\beta }_0+\sum _{i=1}^k{\beta }_i\cdot \text{Spline}(\text{KrankNacht}{)}_i+ϵ$$ Splines ermöglichen es, die Beziehung zwischen KrankNacht und LebenZuf an verschiedenen Punkten der Verteilung unterschiedlich zu gestalten.

3. Interaktionseffekte:

   • Durch die Einführung eines Interaktionsterms zwischen KrankNacht und einer anderen Variablen (z.B. Geschlecht) kann die Wirkung von KrankNacht auf LebenZuf in Abhängigkeit von einer anderen Variable untersucht werden: $$\text{LebenZuf}={\beta }_0+{\beta }_1\cdot \text{KrankNacht}+{\beta }_2\cdot \text{OB5}+{\beta }_3\cdot \text{Geschl}+{\beta }_4\cdot (\text{KrankNacht}\times \text{Geschl})+ϵ$$ Dieser Ansatz ermöglicht es, zu untersuchen, ob der Effekt von KrankNacht auf LebenZuf sich zwischen verschiedenen Geschlechtern unterscheidet.

4. Polynomialer Interaktionsterm:

   • Eine Kombination aus polynominalen Termen und Interaktionstermen kann verwendet werden, um eine noch flexiblere Modellierung zu ermöglichen: $$\text{LebenZuf}={\beta }_0+{\beta }_1\cdot \text{KrankNacht}+{\beta }_2\cdot {\text{KrankNacht}}^2+{\beta }_3\cdot \text{OB5}+{\beta }_4\cdot \text{Geschl}+{\beta }_5\cdot (\text{KrankNacht}\times \text{Geschl})+ϵ$$ Dies ermöglicht es, sowohl nichtlineare Effekte als auch Interaktionen zwischen KrankNacht und Geschlecht zu modellieren.

Diese Methoden bieten flexible Möglichkeiten, die Beziehung zwischen KrankNacht und LebenZuf genauer zu erfassen und komplexe Zusammenhänge in den Daten zu modellieren.

(d) Modell 1.1 wird nun erweitert, indem der Beziehungsstatus als zusätzliche Kovariable in das Modell aufgenommen wird (Modell 1.4). Interpretieren Sie anhand des nachfolgenden R-Outputs das Ergebnis der durchgeführten ANOVA bezüglich der Variable BeziehStat. (2 Punkte)

Modell 1.4

mod1_4 <- lm(LebenZuf ~ Geschl + KrankNacht + OB5 + BeziehStat, data = soep17)
Anova(mod1_4)

Anova Table (Type II tests)
 
Response: LebenZuf
             Sum Sq  Df F value    Pr(>F)
Geschl          1      1  0.2951  0.587
KrankNacht    718      1 276.9838 < 2e-16 ***
OB5           691      1 266.6803 < 2e-16 ***
BeziehStat    631      6  40.5914 < 2e-16 ***
Residuals    33498  13105
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Interpretation der ANOVA für BeziehStat

Die ANOVA-Analyse für Modell 1.4 zeigt die folgende Tabelle für die Variable BeziehStat:

• Sum Sq (Sum of Squares): 631
• Df (Degrees of Freedom): 6
• F value: 40.5914
• Pr(>F) (p-value): < 2e-16 ***

Interpretation

• F-Wert: Der F-Wert von 40.5914 ist sehr hoch, was darauf hinweist, dass die Variable BeziehStat eine signifikante Erklärungskraft für die Lebenszufriedenheit hat.
• p-Wert: Der p-Wert von < 2e-16 ist extrem niedrig, was darauf hindeutet, dass der Effekt von BeziehStat auf die Lebenszufriedenheit statistisch signifikant ist. Dies bedeutet, dass der Beziehungsstatus einen signifikanten Einfluss auf die Lebenszufriedenheit der Teilnehmer hat.

Zusammengefasst zeigt die ANOVA, dass der Beziehungsstatus (BeziehStat) einen signifikanten Beitrag zur Erklärung der Varianz in der Lebenszufriedenheit leistet.

---

Aufgabe 2

Aufgabenstellung

In einer Studie wurden die Schnabellängen (bill_length) der drei in der Antarktis lebenden Pinguinarten Adélie, Chinstrap und Gentoo untersucht. Dabei wurde ein lineares Regressionsmodell (Modell 2.1) geschätzt, das die Schnabellänge durch Haupteffekte für die Pinguinart (species) und das Geschlecht (sex) beschreibt, wobei für beide Kovariablen eine Referenzkodierung verwendet wurde.

Nachfolgend sind die zugehörige Modellgleichung auf Beobachtungsebene (für $i=1,\dots ,333$) sowie der Modelloutput gegeben:

Modell 2.1

$${\text{bill\_length}}_i={\beta }_0+{\beta }_1{\text{species}}_{\text{Chinstrap},i}+{\beta }_2{\text{species}}_{\text{Gentoo},i}+{\beta }_3{\text{sex}}_{\text{male},i}+{ϵ}_i$$

mit ${ϵ}_i\stackrel{iid}{\sim }N(0,{\sigma }^2)$

$${\text{species}}_{\text{Chinstrap},i}=\{\begin{array}{ll}1& {\text{fu¨r species}}_i=\text{Chinstrap}\\ 0& {\text{fu¨r species}}_i\ne \text{Chinstrap}\end{array}$$ $${\text{species}}_{\text{Gentoo},i}=\{\begin{array}{ll}1& {\text{fu¨r species}}_i=\text{Gentoo}\\ 0& {\text{fu¨r species}}_i\ne \text{Gentoo}\end{array}$$ $${\text{sex}}_{\text{male},i}=\{\begin{array}{ll}1& {\text{fu¨r sex}}_i=\text{male}\\ 0& {\text{fu¨r sex}}_i=\text{female}\end{array}$$

mod2_1 <- lm(bill_length ~ species + sex, data = penguins)
summary(mod2_1)

Call:
lm(formula = bill_length ~ species + sex, data = penguins)
 
Residuals:
     Min       1Q   Median       3Q      Max
-6.0869  -1.3770  -0.0709   1.2254  11.0131
 
Coefficients:
                 Estimate Std. Error t value Pr(>|t|)
(Intercept)       36.9770     0.2307 160.25  <2e-16 ***
speciesChinstrap  10.0099     0.3413  29.33  <2e-16 ***
speciesGentoo      8.6975     0.2871  30.29  <2e-16 ***
sexmale            3.6939     0.2548  14.50  <2e-16 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
 
Residual standard error: 2.325 on 329 degrees of freedom
Multiple R-squared:  0.8209,    Adjusted R-squared:  0.8193
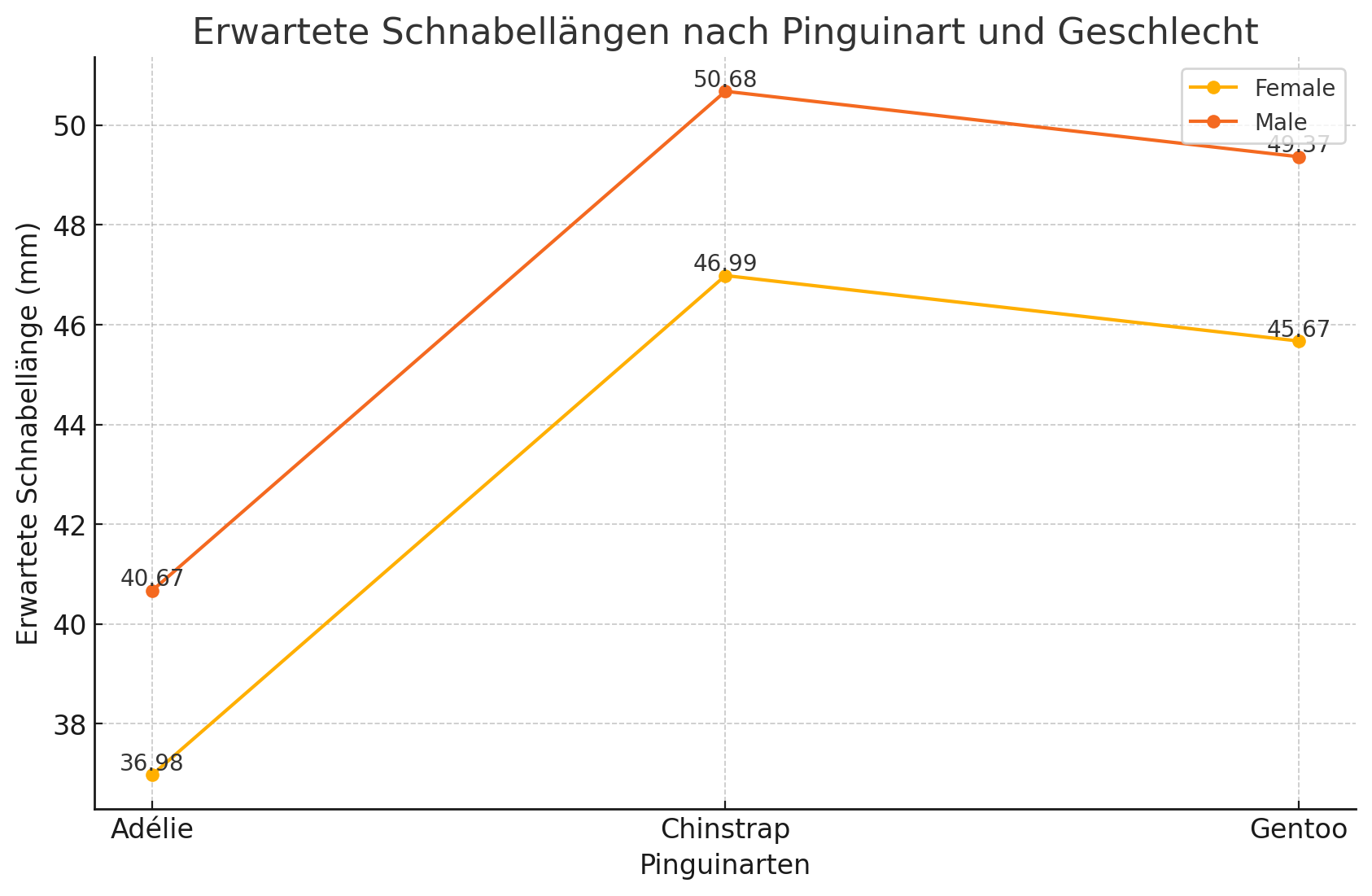
F-statistic: 502.8 on 3 and 329 DF,  p-value: < 2.2e-16

(a) Interpretieren Sie den geschätzten Intercept. (2 Punkte)

• ${\beta }_0$ : (Intercept)
  • Der Intercept ist der Wert wenn alle andern Variablen 0 ist und somit nur die Referenzkategorie gegeben ist
  • In diesem Fall ist die Referenzkategorie die Pinguinart Adelie & Weiblich
  • Die Schnabellänge dieser ist dementsprechend 36.9770 mm

(b) Zeichnen Sie in das nachstehende Diagramm einen Effektplot mit den gemäß Modell 2.1 erwarteten Schnabellängen für die drei Pinguinarten für beide Geschlechter ein. (7 Punkte)

(c) Basierend auf Modell 2.1 soll nun in einem linearen Hypothesentest der Form $A\beta =c$ überprüft werden, ob ein Zusammenhang zwischen der Pinguinart und der Schnabellänge besteht. Geben Sie die Hypothesen für diesen Test, die Matrizen $A$ und $c$ sowie die Verteilung der Teststatistik an. (6 Punkte)

Hypothesen

• Nullhypothese ($H_0$): Es besteht kein Zusammenhang zwischen der Pinguinart und der Schnabellänge.

  $$H_0:{\beta }_1={\beta }_2=0$$

• Alternativhypothese ($H_1$): Es besteht ein Zusammenhang zwischen der Pinguinart und der Schnabellänge.

  $$H_1:{\beta }_1\ne 0\text{ oder }{\beta }_2\ne 0$$

Matrizen $A$ und $c$

Die Hypothesen können in der Form $A\beta =c$ dargestellt werden:

• 2 Zeilen weil zwei Variablen vergleiche ${\beta }_1$ und ${\beta }_2$

• 4 Spalten weil 4 Koeffizienten

• Matrix $A$:

Matrizen:

$$\begin{array}{c}A=\left(\begin{array}{cccc}{\beta }_0& {\beta }_1& {\beta }_2& {\beta }_3\\ {\beta }_0& {\beta }_1& {\beta }_2& {\beta }_3\end{array}\right)=\left(\begin{array}{cccc}0& 1& 0& 0\\ 0& 0& 1& 0\end{array}\right)\in R^{2\times 4}\end{array}$$

Hier stehen die Einträge $1$ an den Positionen, die den Koeffizienten ${\beta }_1$ (speciesChinstrap) und ${\beta }_2$ (speciesGentoo) entsprechen.

• c gibt an, dass ${\beta }_1$ und ${\beta }_2$
• Vektor $c$: $$c=\left(\begin{array}{c}0\\ 0\end{array}\right)$$

Verteilung der Teststatistik

MAN KANN IM R CODE RAUSLESEN

• F(q,p) = F(Anzahl der vergleichenden Koeffizientet, Degrees of Freedom)
• `Residual standard error: 2.325 on 329 degrees of freedom

Die Teststatistik folgt einer $F$-Verteilung, da wir mehrere lineare Einschränkungen testen:

$$F=\frac{(RS{S}_{H_0}-RS{S}_{H_1})/q}{RS{S}_{H_1}/(n-p)}$$

wobei:

• $RS{S}_{H_0}$ der Residual Sum of Squares unter der Nullhypothese ist,
• $RS{S}_{H_1}$ der Residual Sum of Squares unter der Alternativhypothese ist,
• $q$ die Anzahl der Einschränkungen (hier 2),
• $n$ die Anzahl der Beobachtungen,
• $p$ die Anzahl der geschätzten Parameter im Modell unter der Alternativhypothese.

Die Teststatistik $F$ folgt einer $F$-Verteilung mit $q$ und $n-p$ Freiheitsgraden:

$$F\sim F(q,n-p)$$

In diesem Fall:

$$F\sim F(2,329)$$

MAN KANN IM R CODE RAUSLESEN

• F(q,p) = F(Anzahl der vergleichenden Koeffizientet, Degrees of Freedom)
• Residual standard error: 2.325 on 329 degrees of freedom $$F\sim F(2,329)$$

(d) Die Koeffiziententabelle des R-Outputs zu Modell 2.1 enthält ebenfalls Teststatistiken und p-Werte. Erklären Sie, was bei dem Test bezüglich des Koeffizienten zur Pinguinart Chinstrap (zweite Zeile in der Koeffiziententabelle) inhaltlich überprüft wird. (2 Punkte)

Der Test überprüft, ob die durchschnittliche Schnabellänge der Chinstrap-Pinguine signifikant von der der Adélie-Pinguine (Referenzgruppe) abweicht.

Hypothesen

• $H_0:{\beta }_1=0$ (kein Unterschied in der Schnabellänge)
• $H_1:{\beta }_1\ne 0$ (Unterschied in der Schnabellänge)

Teststatistik und p-Wert

• t-Wert: 29.33
• p-Wert: < 2e-16

Interpretation

Der sehr niedrige p-Wert (< 2e-16) zeigt, dass die durchschnittliche Schnabellänge der Chinstrap-Pinguine signifikant von der der Adélie-Pinguine abweicht.

(e) Welche implizite Annahme wurde in Modell 2.1 bezüglich des Effektes der Pinguinart getroffen, indem nur Haupteffekte in das Modell aufgenommen wurden? Erklären Sie anhand des folgenden R-Outputs, ob diese Annahme gerechtfertigt ist. (3 Punkte)

mod2_2 <- lm(bill_length ~ species * sex, data = penguins)
Anova(mod2_2)

Anova Table (Type II tests)
 
Response: bill_length_mm
               Sum Sq Df F value    Pr(>F)
species        6975.6  2 650.4786 < 2e-16 ***
sex            1135.7  1 211.8066 < 2e-16 ***
species:sex      24.5  2   2.2841  0.1035
Residuals      1753.3 327
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Implizite Annahme in Modell 2.1

Die implizite Annahme in Modell 2.1 ist, dass der Effekt der Pinguinart auf die Schnabellänge unabhängig vom Geschlecht ist ( da species + sex und nicht species * sex ) . Das bedeutet, dass keine Interaktion zwischen Pinguinart und Geschlecht berücksichtigt wurde. Die Haupteffekte der Pinguinart und des Geschlechts werden als additiv und unabhängig voneinander angenommen.

Prüfung der Annahme anhand des R-Outputs

Der R-Output von Modell 2.2, welches die Interaktion zwischen Pinguinart und Geschlecht (species * sex) einschließt, zeigt die folgenden Ergebnisse:

Interpretation

• Der p-Wert für die Interaktion species:sex beträgt 0.1035, was größer als das übliche Signifikanzniveau von 0.05 ist.
• Dies bedeutet, dass die Interaktion zwischen Pinguinart und Geschlecht nicht signifikant ist.

Fazit

Die Annahme, dass der Effekt der Pinguinart auf die Schnabellänge unabhängig vom Geschlecht ist, wird durch die ANOVA-Ergebnisse gestützt. Die Interaktion zwischen Pinguinart und Geschlecht ist nicht signifikant, daher ist es gerechtfertigt, nur Haupteffekte in Modell 2.1 zu verwenden.

(f) Bei der Modellierung soll nun für die Pinguinart anstatt der Referenzkodierung eine Effektkodierung verwendet werden, so dass sich die folgende Modellgleichung ergibt:

$$Y_i={\beta }_{0,eff}+{\beta }_{1,eff}{\text{species}}_{\text{Chinstrap},i}+{\beta }_{2,eff}{\text{species}}_{\text{Gentoo},i}+{\beta }_{3,eff}{\text{sex}}_{\text{male},i}+{ϵ}_i$$

mit ${ϵ}_i\sim N(0,{\sigma }^2)$

$${\text{species}}_{\text{Chinstrap},i}=\{\begin{array}{ll}1& {\text{fu¨r species}}_i=\text{Chinstrap}\\ 0& {\text{fu¨r species}}_i=\text{Gentoo}\\ -1& {\text{fu¨r species}}_i=\text{Adelie}\end{array}$$ $${\text{species}}_{\text{Gentoo},i}=\{\begin{array}{ll}0& {\text{fu¨r species}}_i=\text{Chinstrap}\\ 1& {\text{fu¨r species}}_i=\text{Gentoo}\\ -1& {\text{fu¨r species}}_i=\text{Adelie}\end{array}$$ $${\text{sex}}_{\text{male},i}=\{\begin{array}{ll}1& {\text{fu¨r sex}}_i=\text{male}\\ 0& {\text{fu¨r sex}}_i=\text{female}\end{array}$$

Geben Sie die Koeffizienten ${\beta }_{0,eff}$, ${\beta }_{1,eff}$, ${\beta }_{2,eff}$ und ${\beta }_{3,eff}$ an, die man bei einer solchen Kodierung erhalten würde.

Hinweis: Falls Sie bei Teilaufgabe (b) zu keiner Lösung gekommen sind, können Sie die folgenden Ersatzergebnisse für die anhand von Modell 2.1 prädiktierten Gruppenmittelwerte für weibliche Pinguine verwenden: ${\hat{y}}_{Adelie,female}$ = 35.3267, ${\hat{y}}_{Chinstrap,female}$ = 44.6372, ${\hat{y}}_{Gentoo,female}$ = 42.4927.

Lösung

$$Y_i={\beta }_{0,eff}+{\beta }_{1,eff}{\text{species}}_{\text{Chinstrap},i}+{\beta }_{2,eff}{\text{species}}_{\text{Gentoo},i}+{\beta }_{3,eff}{\text{sex}}_{\text{male},i}+{ϵ}_i$$

mit ${ϵ}_i\sim N(0,{\sigma }^2)$

$${\text{species}}_{\text{Chinstrap},i}=\{\begin{array}{ll}1& {\text{fu¨r species}}_i=\text{Chinstrap}\\ 0& {\text{fu¨r species}}_i=\text{Gentoo}\\ -1& {\text{fu¨r species}}_i=\text{Adelie}\end{array}$$ $${\text{species}}_{\text{Gentoo},i}=\{\begin{array}{ll}0& {\text{fu¨r species}}_i=\text{Chinstrap}\\ 1& {\text{fu¨r species}}_i=\text{Gentoo}\\ -1& {\text{fu¨r species}}_i=\text{Adelie}\end{array}$$ $${\text{sex}}_{\text{male},i}=\{\begin{array}{ll}1& {\text{fu¨r sex}}_i=\text{male}\\ 0& {\text{fu¨r sex}}_i=\text{female}\end{array}$$

Berechnung der Koeffizienten

Bei der Effektkodierung werden die Mittelwerte der Kategorien um den Gesamtmittelwert zentriert. Wir können die Koeffizienten basierend auf den gegebenen Gruppenmittelwerten für weibliche Pinguine berechnen.

Gegebene Mittelwerte:

• ${\hat{y}}_{Adelie,female}=35.3267$
• ${\hat{y}}_{Chinstrap,female}=44.6372$
• ${\hat{y}}_{Gentoo,female}=42.4927$

1. Gesamtmittelwert für weibliche Pinguine:

   $${\hat{y}}_{\text{female}}=\frac{{\hat{y}}_{Adelie,female}+{\hat{y}}_{Chinstrap,female}+{\hat{y}}_{Gentoo,female}}{3}$$ $${\hat{y}}_{\text{female}}=\frac{35.3267+44.6372+42.4927}{3}\approx 40.8189$$

2. Berechnung der Koeffizienten:

• ${\beta }_{0,eff}$: Gesamtmittelwert

  $${\beta }_{0,eff}={\hat{y}}_{\text{female}}=40.8189$$

• ${\beta }_{1,eff}$: Effekt von speciesChinstrap (zentriert um den Gesamtmittelwert)

  $${\beta }_{1,eff}={\hat{y}}_{Chinstrap,female}-{\hat{y}}_{\text{female}}=44.6372-40.8189=3.8183$$

• ${\beta }_{2,eff}$: Effekt von speciesGentoo (zentriert um den Gesamtmittelwert)

  $${\beta }_{2,eff}={\hat{y}}_{Gentoo,female}-{\hat{y}}_{\text{female}}=42.4927-40.8189=1.6738$$

• ${\beta }_{3,eff}$: Effekt von sexmale

  $${\beta }_{3,eff}=3.6939\text{ (aus Modell 2.1)}$$

Zusammenfassung der Koeffizienten:

• ${\beta }_{0,eff}=40.8189$
• ${\beta }_{1,eff}=3.8183$
• ${\beta }_{2,eff}=1.6738$
• ${\beta }_{3,eff}=3.6939$

---

Aufgabe 3

Aufgabenstellung

Im Jahr 1969 wurde von Sozialwissenschaftlern in den USA eine Umfrage unter 601 verheirateten Personen durchgeführt, um das Auftreten von außerehelichen Affären zu untersuchen.

Im Rahmen der Studie wurden die folgenden Variablen erhoben:

Variable	Beschreibung
affäre	Affären im letzten Jahr (0 = keine, 1 = mindestens eine)
alter	Alter in Jahren
geschl	Geschlecht
ehejahre	Anzahl der Ehejahre
kinder	Kinder aus der Ehe (ja/nein)

Das Auftreten mindestens einer außerehelichen Affäre im letzten Jahr wird von den Forschern durch Modell 3.1 modelliert:

Modell 3.1

>summary(mod3_1)
 
 
Call:
glm(formula = affäre ~ alter + geschl + ehejahre + kinder, family = binomial(), data = affäre)
 
Deviance Residuals:
     Min        1Q    Median        3Q       Max
-1.0874  -0.7922  -0.6689  -0.4172   2.1313
 
Coefficients:
                Estimate Std. Error z.B.value Pr(>|z|)
(Intercept)    -1.09424    0.42625  -2.567  0.01026 *
alter          -0.03913    0.01730  -2.262  0.02372 *
geschlmännlich  0.32852    0.19915   1.650  0.09902 .
ehejahre        0.09116    0.03070   2.970  0.00298 **
kinderja        0.43480    0.27879   1.560  0.11886
 
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
 
(Dispersion parameter for binomial family taken to be 1)
 
    Null deviance: 675.38  on 600  degrees of freedom
Residual deviance: 653.87  on 596  degrees of freedom
AIC: 663.87
 
Number of Fisher Scoring iterations: 4
 
> exp(coef(m1)[-1])
 
alter  geschlmännlich  ehejahre    kinderja
0.961682  1.388906     1.095449    1.544668

(a) Geben Sie anhand des R-Outputs zu Modell 3.1 die Struktur- und Verteilungsannahme des Modells an. Spezifizieren Sie dabei explizit den linearen Prädiktor. (5 Punkte)

Verteilungsannahme:

• Abhängige Variable ${\text{affa¨re}}_i$ ist binär: 0 (keine Affäre), 1 (mindestens eine Affäre).
• Folgt einer binomialen Verteilung: ${\text{affa¨re}}_i\sim \text{Binomial}(n=1,{\pi }_i)$.
• Die Beobachtungen ${\text{affa¨re}}_i$ sind unabhängig voneinander.

Strukturannahme:

• Logistische Regression wird verwendet.
• Die Wahrscheinlichkeit ${\pi }_i$ wird durch den logistischen Link beschrieben: $\log \left(\frac{{\pi }_i}{1-{\pi }_i}\right)$.

Linearer Prädiktor:

$${\eta }_i=-1.09424-0.03913\cdot {\text{alter}}_i+0.32852\cdot ({\text{geschl}}_{\text{ma¨nnlich}}{)}_i+0.09110\cdot {\text{ehejahre}}_i+0.43480\cdot ({\text{kinder}}_{\text{ja}}{)}_i$$

η_i = -1.09424 - 0.03913 * alter_i + 0.32852 * (geschl_männlich)_i + 0.09110 *
		ehejahre_i + 0.43480 * (kinder_ja)_i

Die geschätzte Wahrscheinlichkeit:

$${\pi }_i=\frac{1}{1+e^{-{\eta }_i}}$$

Zusammenfassung: Das Modell beschreibt die Wahrscheinlichkeit einer Affäre basierend auf Alter, Geschlecht, Ehejahren und Kindern durch eine logistische Verteilung und einen linearen Prädiktor, wobei die Beobachtungen unabhängig voneinander sind.

(b) Interpretieren Sie die geschätzten Koeffizienten der Variablen ehejahre und kinder auf Ebene der Odds. (6 Punkte)

1. Koeffizient für ehejahre (${\beta }_{\text{ehejahre}}=0.09110$):

   • Wenn die Anzahl der Ehejahre um 1 Jahr steigt, erhöhen sich die Chancen für das Auftreten einer Affäre um den Faktor $\exp (0.09110)\approx 1.095$.

2. Koeffizient für kinder (${\beta }_{\text{kinderja}}=0.43480$):

   • Wenn das Ehepaar Kinder hat (ja), erhöhen sich die Chancen für das Auftreten einer Affäre im Mittel (multiplikativ) um den Faktor $\exp (0.43480)\approx 1.544$.

(c) Die Forscher vermuten, dass das Risiko für eine Affäre bei Verheirateten ohne Kinder mit zunehmender Anzahl an Ehejahren steigt, während sie bei Verheirateten mit Kindern sinkt, und passen deshalb Modell 3.2 an.

Modell 3.2

summary(mod3_2)

Call:
glm(formula = affäre ~ alter + geschl + ehejahre * kinder, family = binomial(), data = affäre)
 
Deviance Residuals:
    Min       1Q   Median       3Q      Max
-1.3208  -0.8215  -0.6958  -0.3398   2.1711
 
Coefficients:
                    Estimate Std. Error z.B.value Pr(>|z|)
(Intercept)        -1.52319    0.47267  -3.223  0.001271 **
alter              -0.03826    0.01728  -2.214  0.026810 *
geschlmännlich      0.28215    0.20081   1.405  0.160007
ehejahre            0.12862    0.04332   2.970  0.003000 **
kinderja            1.08262    0.40050   2.703  0.006868 **
ehejahre:kinderja  -0.12956    0.05529  -2.343  0.019118 *
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
 
(Dispersion parameter for binomial family taken to be 1)
 
    Null deviance: 675.38  on 600  degrees of freedom
Residual deviance: 648.49  on 595  degrees of freedom
AIC: 660.49
 
Number of Fisher Scoring iterations: 4

(i) Geben Sie den linearen Prädiktor für Modell 3.2 an. (3 Punkte)

$$\eta ={\beta }_0+{\beta }_1\cdot \text{alter}+{\beta }_2\cdot {\text{geschl}}_{\text{ma¨nnlich}}+{\beta }_3\cdot \text{ehejahre}+{\beta }_4\cdot {\text{kinder}}_{\text{ja}}+{\beta }_5\cdot (\text{ehejahre}\cdot {\text{kinder}}_{\text{ja}})$$

η = β₀ + β₁ ⋅ alter + β₂ ⋅ geschl_männlich + β₃ ⋅ ehejahre + β₄ ⋅ kinder_ja + β₅
	⋅ (ehejahre ⋅ kinder_ja)

(ii) Vergleichen Sie anhand von Modell 3.2 das Risiko ( = der Chance), mindestens eine außereheliche Affäre zu haben, zwischen einer seit sieben Jahren verheirateten 30-jährigen Frau mit Kindern gegenüber einer seit sieben Jahren verheirateten Frau ohne Kinder. (4 Punkte)

• Mit Kindern

  $$\begin{array}{rl}\eta & =-1.52319-0.03826\cdot 30+0.19916\cdot 7+1.08262\cdot 1-0.12956\cdot (7\cdot 1)\\ & =-1.10117\\ & \to e^{-1.10117}=0.33248\end{array}$$

• Ohne Kindern

  $$\begin{array}{rl}\eta & =-1.52319-0.03826\cdot 30+0.19916\cdot 7+1.08262\cdot 0-0.12956\cdot (7\cdot 0)\\ & =-1.27687\\ & \to e^{-1.27687}=0.27890\end{array}$$

Odds:

$$\text{Odds Ratio}=\frac{0.33248}{0.27890}=1.19211$$

→ Es ist rund $19.21\%$ wahrscheinlicher, dass die Frau mit Kindern eine außereheliche Affäre hat gegenüber der Frau ohne Kindern

(iii) Hat gemäß Modell 3.2 ein 30-jähriger Mann, der seit 10 Jahren verheiratet ist, eine höhere Wahrscheinlichkeit für mindestens eine außereheliche Affäre, wenn er Kinder hat oder wenn er keine Kinder hat? Begründen Sie. (3 Punkte)

• Mit Kindern

  $$\begin{array}{rl}\eta & =-1.52319-0.03826\cdot 30+0.28215\cdot 1+0.19916\cdot 10+1.08262\cdot 1-0.12956\cdot (10\cdot 1)\\ & =-0.61022\\ & \to e^{-0.61022}=0.54323\end{array}$$

• Ohne Kindern

  $$\begin{array}{rl}\eta & =-1.52319-0.03826\cdot 30+0.28215\cdot 1+0.19916\cdot 10+1.08262\cdot 0-0.12956\cdot (10\cdot 0)\\ & =-0.39724\\ & \to e^{-0.39724}=0.67217\end{array}$$

Odds:

$$\text{Odds Ratio}=\frac{0.54323}{0.67217}=0.80817$$

→ Es ist rund $20\%$ unwahrscheinlicher, dass der Mann mit Kindern verglichen zu dem ohne Kindern fremdgeht

---

Aufgabe 4

Aufgabenstellung

Im Rahmen dieser Aufgabe soll der in der Einheit Meilen pro Gallone gemessene Benzinverbrauch von historischen US-amerikanischen Fahrzeugen (mpg) in Abhängigkeit verschiedener Kovariablen modelliert werden. Die folgende Tabelle gibt eine Übersicht über alle potenziell zur Verfügung stehenden Kovariablen:

Variable	Beschreibung
zyl	Anzahl der Zylinder
disp	Hubraum (in Kubikzoll)
hp	Motorleistung (in PS)
drat	Hinterachsübersetzung
wt	Gewicht (in 1000 Pfund)
qsec	Zeit, die für eine Viertelmeile benötigt wird
vs	Motor (0 = V-förmig, 1 = Gerade)
am	Getriebe (0 = Automatik, 1 = Manuell)
gear	Anzahl der Vorwärtsgänge
carb	Anzahl der Vergaser

(a) Zunächst wird ein lineares Modell geschätzt, bei dem alle zehn möglichen Einflussgrößen berücksichtigt werden (Modell 4.1):

Modell 4.1

> summary(mod4_1)
 
 
Call:
lm(formula = mpg ~ ., data = mtcars)
 
Residuals:
    Min      1Q  Median      3Q     Max
-3.4506 -1.6044 -0.1196  1.2193  4.6271
 
Coefficients:
            Estimate Std. Error t value Pr(>|t|)
(Intercept)  12.30337   18.71788   0.657  0.5181
cyl          -0.11144    1.04502  -0.107  0.9161
disp          0.01334    0.01786   0.747  0.4635
hp           -0.02148    0.02177  -0.987  0.3350
drat         -0.78711    1.63537  -0.481  0.6353
wt           -3.71530    1.89441  -1.961  0.0633
qsec          0.82104    0.73084   1.123  0.2739
vs            0.31776    2.10451   0.151  0.8814
am            2.52023    2.05665   1.226  0.2340
gear          0.65541    1.49326   0.439  0.6652
carb         -0.19942    0.82875  -0.241  0.8122
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
 
Residual standard error: 2.65 on 21 degrees of freedom
Multiple R-squared:  0.869,    Adjusted R-squared:  0.8066
F-statistic: 13.93 on 10 and 21 DF,  p-value: 3.793e-07

i) Beurteilen Sie anhand des Modelloutputs die Modellgüte von Modell 4.1. (2 Punkte)

1. Multiple R-squared: Der Wert beträgt 0.869, was bedeutet, dass 86.9% der Varianz im Benzinverbrauch (mpg) durch die erklärenden Variablen des Modells erklärt werden. Dies zeigt eine sehr gute Anpassung des Modells an die Daten.
2. Adjusted R-squared: Der Wert beträgt 0.8066. Dieser Wert berücksichtigt die Anzahl der Prädiktoren und die Stichprobengröße und bestätigt die hohe Modellgüte.
3. F-statistic und p-Wert: Die F-statistic beträgt 13.93 mit einem p-Wert von 3.793e-07. Der extrem niedrige p-Wert zeigt, dass das Modell insgesamt statistisch signifikant ist, was bedeutet, dass die Kovariablen gemeinsam einen signifikanten Einfluss auf den Benzinverbrauch haben.
4. Residual standard error (RSE): Der Wert beträgt 2.65. Dies zeigt die durchschnittliche Abweichung der vorhergesagten Werte von den tatsächlichen Werten und ist akzeptabel in Bezug auf die Skala der abhängigen Variable (mpg).

Fazit: Modell 4.1 zeigt eine sehr gute Anpassung an die Daten (hohe R-squared-Werte) und ist statistisch signifikant (sehr niedriger p-Wert des F-Tests).

ii) Begründen Sie anhand des Outputs zu Modell 4.1, warum für die Modellierung des Benzinverbrauchs die Durchführung einer Variablenselektion sinnvoll sein könnte. (3 Punkte)

1. Nicht-signifikante Koeffizienten: Viele Variablen im Modell 4.1 haben p-Werte > 0.05 (z.B. $\text{cyl}$, $\text{disp}$, $\text{hp}$, $\text{drat}$, $\text{qsec}$, $\text{vs}$, $\text{am}$, $\text{gear}$, $\text{carb}$), was darauf hinweist, dass sie keinen signifikanten Einfluss auf den Benzinverbrauch haben.

2. Überparametisiert: Ein Modell mit zu vielen Parametern, insbesondere solchen, die keinen signifikanten Einfluss haben, ist überparametisiert. Dies führt zu unnötiger Komplexität und kann die Generalisierbarkeit des Modells verschlechtern.

3. Multikollinearität: Überflüssige Variablen können zu Multikollinearität führen, was die Schätzungen der Koeffizienten instabil und das Modell schwer interpretierbar macht.

4. Modelleffizienz: Ein Modell mit weniger, aber signifikanten Variablen ist effizienter und leichter interpretierbar, ohne die Vorhersagekraft zu beeinträchtigen.

Fazit: Eine Variablenselektion verbessert die Interpretierbarkeit und Stabilität des Modells, indem sie sich auf die wesentlichen Prädiktoren konzentriert und überflüssige, nicht-signifikante Variablen entfernt. Dies vermeidet eine Überparametisierung und erhöht die Effizienz des Modells.

iii) Verwenden Sie die zuvor berechneten AICs, um Modell 4.1 mit Modell 4.2 zu vergleichen. Welches Modell würden Sie anhand dieses Kriteriums bevorzugen? Begründen Sie. (2 Punkte)

Antwort fehlt.

Hinweis: Falls Sie bei Teilaufgabe (b)(ii) zu keiner Lösung gekommen sind, können Sie die folgenden Ersatzergebnisse für die AICs zu Modell 4.1 und Modell 4.2 verwenden: $AI{C}_{4.1}=165$, $AI{C}_{4.2}=155$.

Bewertung: 0/2 Punkten

(d) Begründen Sie, warum ein schrittweiser Variablenselektionsprozess für die gegebene Datensituation gegenüber der Best Subset-Methode mit einem Vergleich aller möglichen Modelle vorteilhaft sein könnte. (2 Punkte)

• Schrittweise Variablenselektionsprozess:
  • Rechenintensität: Weniger rechenintensiv und schneller als die Best Subset-Methode.
  • Anwendung: Einfacher in der Anwendung, da Variablen schrittweise hinzugefügt oder entfernt werden.
  • Flexibilität: Bietet flexible Selektionskriterien und Methoden (vorwärts, rückwärts, beides).

Fazit: Die schrittweise Variablenselektion ist hier besser geeignet, da die Best-Subset Methode bei 10 Variablen sehr viele Kombinationen ($2^{10}=1024$) ausprobieren müsste, was viel zu rechenintensiv und zeitaufwendig wäre.

(e) Begründen Sie in Ihren eigenen Worten, warum es problematisch ist, eine Variablenselektion anhand von p-Werten durchzuführen. (4 Punkte)

• Überanpassung (Overfitting):

  • Auswahl der Variablen nur nach p-Werten kann zu spezifischen Anpassungen an die Trainingsdaten führen
  • Schlechte Generalisierbarkeit auf neue Daten

• Instabilität der p-Werte:

  • p-Werte können sich stark ändern, wenn sich die Auswahl der anderen Variablen ändert
  • Hohe Empfindlichkeit gegenüber kleinen Datenänderungen

• Multikollinearität:

  • Hohe Korrelation zwischen Variablen kann p-Werte irreführend machen
  • Signifikanz einzelner Variablen kann falsch eingeschätzt werden

• Vernachlässigung der Modellstruktur und -theorie:

  • Fokussierung auf p-Werte vernachlässigt theoretische und praktische Überlegungen
  • Ein gutes Modell sollte auch auf inhaltlichem Wissen basieren

Fazit: Variablenselektion nur nach p-Werten kann zu überangepassten, instabilen und theoretisch nicht fundierten Modellen führen.

---

Aufgabe 5

Die folgenden Aufgabenstellungen stellen offene Fragen dar, die in Textform beantwortet werden sollen. Achten Sie dabei insbesondere darauf, dass Sie Ihre eigenen Worte verwenden:

(a) Erläutern Sie den Unterschied zwischen partiellen und sequentiellen Quadratsummen am Beispiel eines Regressionsmodells $Y={\beta }_0+{\beta }_1{x}_1+{\beta }_2{x}_2+ϵ$. Welche Modelle werden bei der Bestimmung der Quadratsummen jeweils betrachtet? (5 Punkte)

• Partielle Quadratsumme:

  • Zusätzliche Erklärungskraft eines Prädiktors
  • Alle anderen Prädiktoren bereits im Modell
  • Beispiel: Bei $Y={\beta }_0+{\beta }_1{x}_1+{\beta }_2{x}_2+ϵ$ betrachtet die partielle Quadratsumme von $x_2$, wie viel zusätzliche Varianz in $Y$ durch $x_2$ erklärt wird, nachdem $x_1$ bereits im Modell ist.

• Sequentielle Quadratsumme:

  • Hängt von der Reihenfolge der Prädiktoren im Modell ab
  • Zusätzliche Erklärungskraft eines Prädiktors, wenn er als letzter eingefügt wird
  • Beispiel:
    • Wenn $x_1$ zuerst und $x_2$ danach eingefügt werden, betrachtet die sequentielle Quadratsumme von $x_2$ die zusätzliche Varianz, die $x_2$ erklärt, nachdem $x_1$ bereits im Modell ist.
    • Umgekehrt, wenn $x_2$ zuerst und $x_1$ danach eingefügt wird, betrachtet die sequentielle Quadratsumme von $x_1$ die zusätzliche Varianz, die $x_1$ erklärt, nachdem $x_2$ bereits im Modell ist.

Die partielle Quadratsumme betrachtet die zusätzliche Erklärungskraft eines Prädiktors, nachdem alle anderen Prädiktoren bereits im Modell sind. Beispielsweise bei $Y={\beta }_0+{\beta }_1{x}_1+{\beta }_2{x}_2+ϵ$ betrachtet die partielle Quadratsumme von $x_2$, wie viel zusätzliche Varianz in $Y$ durch $x_2$ erklärt wird, nachdem $x_1$ bereits im Modell ist.

Die sequentielle Quadratsumme hingegen hängt von der Reihenfolge ab, in der die Prädiktoren in das Modell eingefügt werden. Sie betrachtet die zusätzliche Erklärungskraft eines Prädiktors, wenn er als letzter in das Modell eingefügt wird. Wenn $x_1$ zuerst und $x_2$ danach eingefügt werden, betrachtet die sequentielle Quadratsumme von $x_2$ die zusätzliche Varianz, die $x_2$ erklärt, nachdem $x_1$ bereits im Modell ist. Umgekehrt, wenn $x_2$ zuerst und $x_1$ danach eingefügt wird, betrachtet die sequentielle Quadratsumme von $x_1$ die zusätzliche Varianz, die $x_1$ erklärt, nachdem $x_2$ bereits im Modell ist.

(b) Das Einkommen von Akademikern soll in einem linearen Modell u.a. anhand der Fachrichtung ihres Studiums modelliert werden, wobei für diese insgesamt 15 Kategorien vorliegen. Im Modelloutput wird ersichtlich, dass die Fachrichtung einen signifikanten Einfluss hat. Um Unterschiede zwischen einzelnen Fachrichtungen zu untersuchen, sollen nun paarweise Hypothesentests zwischen allen Fachrichtungen durchgeführt werden. Erläutern Sie, welche Problematik hierbei auftritt. Beschreiben Sie eine mögliche Strategie, um damit umgehen zu können. (5 Punkte)

• Problem der multiplen Tests:

  • Erhöht die Wahrscheinlichkeit eines Fehler 1. Art (fälschlicherweise signifikant)
  • 105 paarweise Tests $((\genfrac{}{}{0ex}{}{15}{2})=105)$
  • Wahrscheinlichkeit für Fehler steigt stark an

• Strategien zur Handhabung:

  • Bonferroni-Korrektur:

    • Signifikanzniveau (\alpha) durch Anzahl der Tests teilen
    • Adjustiertes Signifikanzniveau für jeden Test

  • Methoden zur Kontrolle der falschen Entdeckungsrate (FDR):

    • Benjamini-Hochberg-Prozedur:
      • Weniger konservative Anpassung
      • Erhöht die Testmacht

Bei paarweisen Hypothesentests zwischen allen Fachrichtungen tritt das Problem der multiplen Tests auf, welches die Wahrscheinlichkeit erhöht, dass zumindest ein Test fälschlicherweise signifikant wird (Fehler 1. Art). Da es insgesamt $\left(\genfrac{}{}{0ex}{}{15}{2}\right)=105$ paarweise Tests gibt, steigt die Wahrscheinlichkeit eines oder mehrerer Fehler stark an.

Eine mögliche Strategie zur Handhabung dieses Problems ist die Bonferroni-Korrektur, bei der das Signifikanzniveau $\alpha$ durch die Anzahl der Tests geteilt wird, um das adjustierte Signifikanzniveau für jeden einzelnen Test zu bestimmen. Eine weitere Möglichkeit ist die Verwendung von Methoden zur Kontrolle der falschen Entdeckungsrate (False Discovery Rate, FDR), wie die Benjamini-Hochberg-Prozedur, die eine weniger konservative Anpassung vornimmt und somit die Testmacht erhöht.

(c) Erklären Sie den Unterschied zwischen einflussreichen Beobachtungen und Ausreißern bei einem linearen Regressionsmodell. Erklären Sie jeweils, wie solche Beobachtungen im Rahmen der Modelldiagnose identifiziert werden können. (4 Punkte)

• Einflussreiche Beobachtungen:

  • Datenpunkte mit großem Einfluss auf die Schätzung der Regressionskoeffizienten
  • Identifikation durch Cook’s D-Wert
  • Hohe Cook’s D-Werte deuten auf starke Beeinflussung der Koeffizienten hin

• Ausreißer:

  • Datenpunkte, die stark von den anderen abweichen
  • Können die Modellanpassung verschlechtern
  • Identifikation durch Analyse der Residuen (z.B. studentisierte Residuen)
  • Hohe absolute Residuenwerte weisen auf Ausreißer hin

• Unterschiede und Gemeinsamkeiten:

  • Einflussreiche Beobachtungen müssen keine hohen Residuen haben
  • Ausreißer können hohe Residuen haben, ohne die Koeffizienten stark zu beeinflussen
  • Beide sollten sorgfältig untersucht werden
  • Maßnahmen zur Minderung ihrer Auswirkungen sind gegebenenfalls erforderlich

Einflussreiche Beobachtungen sind Datenpunkte, die einen großen Einfluss auf die Schätzung der Regressionskoeffizienten haben. Sie werden oft durch den Cook’s D-Wert identifiziert, wobei hohe Werte auf eine starke Beeinflussung der Koeffizienten hindeuten.

Ausreißer sind Datenpunkte, die stark von den anderen Datenpunkten abweichen und die Modellanpassung verschlechtern können. Sie werden oft durch die Untersuchung der Residuen identifiziert, zum Beispiel durch die Analyse der studentisierten Residuen, wobei hohe absolute Werte auf Ausreißer hinweisen.

Während einflussreiche Beobachtungen die Koeffizienten stark beeinflussen können, müssen sie keine hohen Residuen haben. Ausreißer können hohe Residuen haben, ohne die Koeffizienten stark zu beeinflussen. Beide Arten von Beobachtungen sollten sorgfältig untersucht und gegebenenfalls Maßnahmen ergriffen werden, um ihre Auswirkungen zu mindern.

(d) In einer Studie absolvieren 30 ProbandInnen über einen Zeitraum von einem Jahr einmal im Monat einen Sporttest. Die erzielten Punkte sollen durch ein Regressionsmodell anhand der absolvierten Trainingseinheiten im jeweiligen Monat beschrieben werden. Bei der Modellierung wird zunächst ignoriert, dass sich die Daten aus wiederholten Messungen an denselben Personen zusammensetzen, und ein lineares Modell $Y=X\beta +ϵ$ mit $ϵ\sim N(0,{\sigma }^{2}I)$ geschätzt.

(i) Bei der Modelldiagnose fällt auf, dass die Residuen innerhalb der einzelnen ProbandInnen immer sehr ähnliche Werte aufweisen. Welche Annahme des linearen Modells ist in diesem Fall verletzt? Beschreiben Sie einen Modellierungsansatz, mit dem diese Problematik behoben werden kann. Nennen Sie ein Verfahren, mit dem das Modell geschätzt werden kann. (5 Punkte)

• Verletzung der Annahme der Unabhängigkeit der Fehler:

  • Residuen innerhalb der einzelnen ProbandInnen sind korreliert

• Lösung durch gemischtes Modell (Mixed-Effects Modell):

  • Berücksichtigt zufällige Effekte für die ProbandInnen

• Modellformulierung:

  • $$Y_{ij}={\beta }_0+{\beta }_1{X}_{ij}+u_i+{ϵ}_{ij}$$
  • $u_i$: Zufällige Effekte für den $i$-ten Probanden
  • ${ϵ}_{ij}$: Verbleibende Fehler

• Schätzungsmethode:

  • Restricted Maximum Likelihood (REML) Methode

Die Annahme der Unabhängigkeit der Fehler ist in diesem Fall verletzt, da die Residuen innerhalb der einzelnen ProbandInnen korreliert sind. Um diese Problematik zu beheben, kann ein gemischtes Modell (Mixed-Effects Modell) verwendet werden, das zufällige Effekte für die ProbandInnen berücksichtigt. Das Modell kann in folgender Form geschrieben werden:

$$Y_{ij}={\beta }_0+{\beta }_1{X}_{ij}+u_i+{ϵ}_{ij}$$

wobei $u_i$ die zufälligen Effekte für den $i$-ten Probanden und ${ϵ}_{ij}$ die verbleibenden Fehler sind. Dieses Modell kann mittels der Restricted Maximum Likelihood (REML) Methode geschätzt werden.

(ii) Zusätzlich soll nun auch noch berücksichtigt werden, dass die Streuung der Residuen für die einzelnen ProbandInnen unterschiedlich groß ist. Kann die Modellierung in diesem Fall noch mit dem in der vorherigen Teilaufgabe beschriebenen Modell erfolgen? Begründen Sie. (2 Punkte)

• Problem mit dem bisherigen Modell:

  • Annahme homoskedastischer Fehler (gleiche Varianz der Residuen für alle ProbandInnen)

• Erweiterung zur Berücksichtigung heteroskedastischer Fehler:

  • Verwendung eines erweiterten gemischten Modells
  • Schätzung der Varianzkomponenten separat für jeden Probanden

• Alternative Methode:

  • Generalized Least Squares (GLS) Ansatz
  • Modellierung unterschiedlicher Varianzen

• Vorteil des erweiterten gemischten Modells und GLS:

  • Berücksichtigung der Heteroskedastizität (unterschiedliche Varianz der Residuen)

Nein, das Modell aus der vorherigen Teilaufgabe ist nicht ausreichend, da es homoskedastische Fehler annimmt (gleiche Varianz der Residuen für alle ProbandInnen). Um heteroskedastische Fehler zu berücksichtigen, kann ein erweitertes gemischtes Modell verwendet werden, das Varianzkomponenten für jeden Probanden separat schätzt. Alternativ kann ein Generalized Least Squares (GLS) Ansatz verwendet werden, der unterschiedliche Varianzen modellieren kann.

---