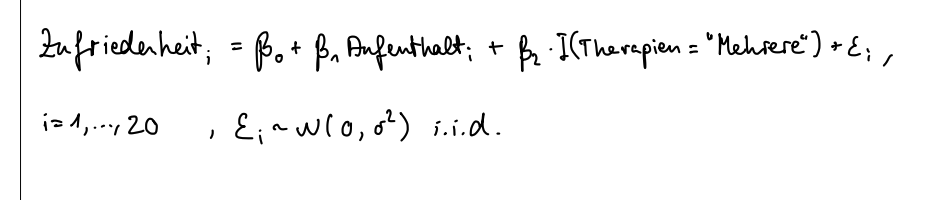Klausur (Probeklausur 2 Sommersemester 2024) - Lineare Modelle

---

AUFGABENTYPEN - PK2

Modellgleichungen und Interpretation

1. Aufgabe 1

   • (a) Modellgleichung aufstellen
   • (b) Interpretation der Koeffizienten

2. Aufgabe 3

   • (a) Linearer Prädiktor, Responsefunktion und Verteilung der Zielvariable
   • (b) Interpretation der Koeffizienten auf Ebene der Odds
   • (c) Vergleich der Chancen für Kreditkartenbewilligung

3. Aufgabe 4

   • (a) Interpretation des $R^2$

Berechnungen und Konfidenzintervalle

4. Aufgabe 1

   • (c) Erwartete Zufriedenheit berechnen

5. Aufgabe 4

   • (ii) RMSE für Prognose neuer Daten
   • (iii) Grund für gleiche RMSEs

Modellannahmen und -überprüfung

6. Aufgabe 1

   • (d) Überprüfung der Linearität
   • (e) Überprüfung der Normalverteilungsannahme

7. Aufgabe 3

   • (d) Problematik der Variable expenditure

8. Aufgabe 4

   • (d) Vorteile der schrittweisen Variablenselektion gegenüber Best Subset-Methode

Hypothesentests und Modellvergleich

9. Aufgabe 2

   • (c) Hypothesentest der Bildungskategorien
   • (f) Veränderung des Bildungseffekts über Zeit überprüfen

10. Aufgabe 4

• (b) Variablenselektionsverfahren analysieren
  • (i) Bestimmung des Selektionskriteriums und -methode
  • (ii) Verfahren für das kleinste Modell
  • (iii) RMSE für Prognose neuer Daten
  • (iv) Grund für gleiche RMSEs
• (d) Variablenselektion mit $R^2$ als Kriterium

Datensituationen und Modellanpassungen

11. Aufgabe 2

• (d) Vorteile des Random Intercept-Modells
• (e) Intra-Class-Correlation berechnen und interpretieren

12. Aufgabe 5

• (a) Beurteilung der Varianzhomogenitäts- und Normalverteilungsannahme
• (b) Problematik der Kollinearität
• (c) Unterschied zwischen Konfidenz- und Prognoseintervall
• (d) Anwendung eines gemischten linearen Modells
• (e) Eignung der logistischen Regression zur Vorhersage von Wahrscheinlichkeiten

Datenvisualisierung und Interpretation

13. Aufgabe 3

• (e) ROC-Kurve zeichnen und AUC berechnen

---

INHALTSVERZEICHNIS - PK2

1. Aufgabe 1

   • (a) Modellgleichung aufstellen
   • (b) Interpretation der Koeffizienten
   • (c) Erwartete Zufriedenheit berechnen
   • (d) Überprüfung der Linearität
   • (e) Überprüfung der Normalverteilungsannahme

2. Aufgabe 2

   • (a) Referenzkategorie und Begründung
   • (b) Bestimmung der geschätzten Koeffizienten
   • (c) Hypothesentest der Bildungskategorien
   • (d) Vorteile des Random Intercept-Modells
   • (e) Intra-Class-Correlation berechnen und interpretieren
   • (f) Veränderung des Bildungseffekts über Zeit überprüfen

3. Aufgabe 3

   • (a) Linearer Prädiktor, Responsefunktion und Verteilung der Zielvariable
   • (b) Interpretation der Koeffizienten auf Ebene der Odds
   • (c) Vergleich der Chancen für Kreditkartenbewilligung
   • (d) Problematik der Variable expenditure
   • (e) ROC-Kurve zeichnen und AUC berechnen

4. Aufgabe 4

   • (a) Interpretation des $R^2$
   • (b) Variablenselektionsverfahren analysieren
     • (i) Bestimmung des Selektionskriteriums und -methode
     • (ii) Verfahren für das kleinste Modell
     • (iii) RMSE für Prognose neuer Daten
     • (iv) Grund für gleiche RMSEs
   • (c) Vor- und Nachteile der schrittweisen Variablenselektion
   • (d) Variablenselektion mit $R^2$ als Kriterium

5. Aufgabe 5

   • (a) Beurteilung der Varianzhomogenitäts- und Normalverteilungsannahme
   • (b) Problematik der Kollinearität
   • (c) Unterschied zwischen Konfidenz- und Prognoseintervall
   • (d) Anwendung eines gemischten linearen Modells
   • (e) Eignung der logistischen Regression zur Vorhersage von Wahrscheinlichkeiten

---

Aufgabe 1

Aufgabenstellung

Ein Krankenhaus untersucht Faktoren, die die Zufriedenheit von PatientInnen (Zufriedenheit) beeinflussen könnten. Die Zufriedenheit wird über einen standardisierten Fragebogen auf einer Skala von 1 (sehr unzufrieden) bis 5 (sehr zufrieden) erfasst.

Als mögliche Einflussfaktoren werden die Variablen Aufenthalt und Therapien betrachtet. Die Variable Aufenthalt gibt die Dauer des Krankenhausaufenthalts in Tagen an. Die binäre Variable Therapien mit den Ausprägungen NurEine und Mehrere gibt an, ob ein Patient nur eine oder mehrere unterschiedliche Therapien im Krankenhaus erhalten hat.

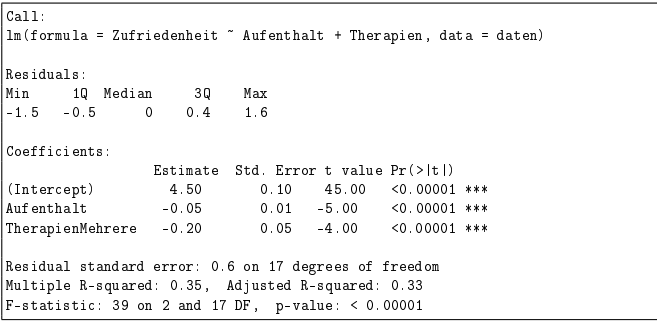
Im Folgenden ist der R-Output eines multiplen linearen Regressionsmodells für einen Datensatz mit 20 PatientInnen (Modell 1.1) gegeben:

Modell 1.1

(a) Stellen Sie anhand des R-Outputs die Modellgleichung zu Modell 1.1 auf.

Eugens Lösung

Ohne Werte:

$$\text{Zufriedenheit}={\beta }_0+{\beta }_1\cdot \text{Aufenthalt}+{\beta }_2\cdot \text{TherapienMehrere}+\epsilon$$

Mit Werten:

$$\text{Zufriedenheit}=4.5+-0.05\cdot \text{Aufenthalt}+-0.20\cdot \text{TherapienMehrere}$$

(b) Interpretieren Sie die Koeffizienten der Variablen Aufenthalt und Therapien.

Eugens Lösung

Wenn sich des Aufenthelt um einen Tag verlängert dann sinkt die Zufriedenheit ceteris paribus im Durchschnitt um 0.05 Einheiten. Wenn der Patient mehrere Therapien erhält, dann sinkt dessen Zufriedenheit im Vergleich zu einem Patienten der nur eine Therapie erhalt im Durchschnitt Ceteris paribus um 0.2 Einheiten.

• Aufenthalt
  • Pro Tag um den sich der Aufenthalt im Krankenhaus verlängert, sinkt die Zufriedenheit um -0.5
• TherapienMehrere
  • Ist eine Binärvariable
  • Falls ein Patient mehrere Therapien hat, wirkt sich dies mit -0.20 Einheiten negativ auf seine allgemeine Zufriedenheit aus.

(c) Ein Patient hatte einen Krankenhausaufenthalt von sieben Tagen und benötigte drei Therapien. Wie hoch ist die erwartete Zufriedenheit dieses Patienten gemäß Modell 1.1?

$$\begin{array}{rl}\text{Therapien}& =4.5+-0.05\cdot 7+-0.20\cdot 1\\ & =3.95\end{array}$$

(d) Es ist zweifelhaft, ob der Zusammenhang zwischen der Dauer des Aufenthalts und der Zufriedenheit linear ist. Nennen und beschreiben Sie zwei sinnvolle Modifikationen des Modells, mit deren Hilfe die Linearität überprüft werden kann.

Eugens Lösungen

Um die Linearität zu überprüfen, können folgende Modifikationen des Modells vorgenommen werden:

• 1. Quadratischer Term - Ein quadratischer Term kann hinzugefügt werden, um nichtlineare Beziehungen zu erfassen:

  $$\text{Zufriedenheit}={\beta }_0+{\beta }_1\cdot \text{Aufenthalt}+{\beta }_2\cdot {\text{Aufenthalt}}^2+{\beta }_3\cdot \text{TherapienMehrere}+\epsilon$$

  - Wenn $\beta_2$ signifikant ist, deutet dies auf eine nichtlineare Beziehung hin.
  

• 2. Splines oder Stückweise Regression - Durch die Verwendung von Splines kann der Zusammenhang in verschiedene Abschnitte unterteilt werden:

  $$\text{Zufriedenheit}={\beta }_0+{\beta }_1\cdot {\text{Aufenthalt}}_{\text{Segment 1}}+{\beta }_2\cdot {\text{Aufenthalt}}_{\text{Segment 2}}+{\beta }_3\cdot \text{TherapienMehrere}+\epsilon$$

  - Signifikante Unterschiede zwischen den Segmenten deuten auf eine nichtlineare Beziehung hin.
  

(e) Beschreiben Sie eine Möglichkeit, wie die Normalverteilungsannahme bei einem linearen Modell überprüft werden kann. Welche Problematik könnte sich bei Modell 1.1 bezüglich dieser Annahme ergeben?

Stichpunkte

• Möglichkeit zur Überprüfung der Normalverteilungsannahme:

  • Erstellung eines Q-Q-Plots der Residuen
  • Vergleich der Verteilung der Residuen mit einer theoretischen Normalverteilung
  • Punkte im Q-Q-Plot sollten annähernd auf einer Geraden liegen

• Problematik bei Modell 1.1:

  • Zufriedenheitswerte auf einer Skala von 1 bis 5 könnten nicht normalverteilt sein
  • Kleine Stichprobengröße (20 Patienten) könnte Normalverteilungsannahme der Residuen verletzen
  • Verletzung der Normalverteilungsannahme könnte Testergebnisse und Konfidenzintervalle beeinflussen
  • Verteilung könnte z.B stattdessen schief, bimodal oder diskret sein
  • Hier: Therapien ist kategorisch behandelt. Dies führt zur diskreten Darstellung der Datenpunkte und erschwert die Erkennung der Normalverteilung.

Fließtext

Eine Möglichkeit, die Normalverteilungsannahme bei einem linearen Modell zu überprüfen, besteht in der Erstellung eines Q-Q-Plots der Residuen. Dieser Plot vergleicht die Verteilung der Residuen mit einer theoretischen Normalverteilung. Liegen die Punkte im Q-Q-Plot annähernd auf einer Geraden, so ist die Normalverteilungsannahme plausibel.

Bei Modell 1.1 könnte sich eine Problematik ergeben, da die Zufriedenheitswerte auf einer Skala von 1 bis 5 möglicherweise nicht normalverteilt sind. Zudem könnte die kleine Stichprobengröße von 20 Patienten die Normalverteilungsannahme der Residuen verletzen. Diese Verletzung könnte die Validität der Testergebnisse und Konfidenzintervalle beeinträchtigen.

---

Aufgabe 2

Aufgabenstellung

Im Jahr 2018 wurde im Rahmen einer Umfrage zum Reiseverhalten in Deutschland bei 1000 Personen unter anderem die Entfernung des Reiseziels vom Wohnort bei der wichtigsten Reise des Jahres (Reisedistanz) erhoben.

Bei der Analyse der Daten wurde ein lineares Regressionsmodell (Modell 2.1) geschätzt, das die Reisedistanz in Abhängigkeit des Alters (Alter), des monatlichen Nettoeinkommens in 1000 € (Einkommen) und des Bildungsniveaus (Bildung) beschreibt. Das Bildungsniveau wurde hierzu in drei Kategorien niedrig (kein Schulabschluss, Hauptschulabschluss), mittel (Mittlere Reife) und hoch (Abitur, Hochschulabschluss) eingeteilt.

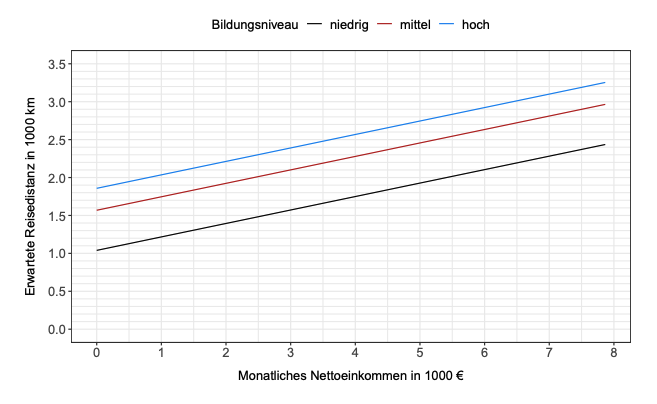
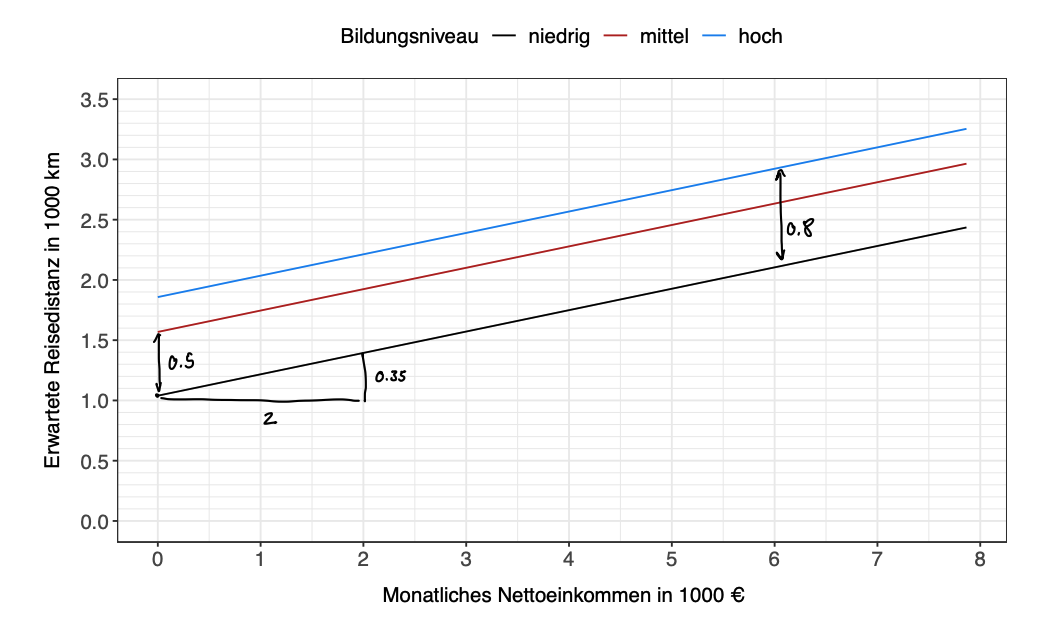
Nachfolgend sind die zugehörige Modellgleichung auf Beobachtungsebene sowie ein Effektplot der Variable Einkommen getrennt nach den Bildungsniveaus für eine 30-jährige Person gegeben:

Modell 2.1

$$Reisedistan{z}_i={\beta }_0+{\beta }_{1}Alte{r}_i+{\beta }_{2}Einkomme{n}_i+{\beta }_{3}Bildun{g}_{mittel,i}+{\beta }_{4}Bildun{g}_{hoch,i}+{ϵ}_i$$

mit ${ϵ}_i\stackrel{iid}{\sim }N(0,{\sigma }^2)$,

$$Bildun{g}_{mittel,i}=\{\begin{array}{ll}1& {\text{fu¨r Bildung}}_i=\text{mittel}\\ 0& {\text{fu¨r Bildung}}_i\ne \text{mittel}\end{array}$$ $$Bildun{g}_{hoch,i}=\{\begin{array}{ll}1& {\text{fu¨r Bildung}}_i=\text{hoch}\\ 0& {\text{fu¨r Bildung}}_i\ne \text{hoch}\end{array}$$

(a) Geben Sie die Referenzkategorie der Variable Bildung an und begründen Sie, warum diese eine sinnvolle Wahl darstellt.

Stichpunkte

• Referenzkategorie:

  • niedrig

• Begründung:

  • niedrig bildet die Ausgangsbasis
  • Vergleich der Kategorien mittel und hoch mit der Basis
  • Erleichtert die Interpretation der Unterschiede zwischen den Bildungsniveaus

Fließtext

Die Referenzkategorie der Variable Bildung ist niedrig. Dies ist eine sinnvolle Wahl, weil niedrig die Ausgangsbasis bildet, mit der die anderen Kategorien (mittel und hoch) verglichen werden. Indem niedrig als Referenz genommen wird, können die Effekte von mittlerer und hoher Bildung direkt interpretiert werden, indem sie die Abweichungen von der Basis (niedrige Bildung) darstellen. Dies erleichtert die Interpretation der Unterschiede zwischen den Bildungsniveaus.

(b) Bestimmen Sie anhand des Effektplots die geschätzten Koeffizienten ${\beta }_0$, ${\beta }_2$, ${\beta }_3$ und ${\beta }_4$, wobei ${\hat{\beta }}_1=-0.0076$ als bekannt vorausgesetzt wird.

$$\begin{array}{rl}{\hat{\beta }}_0& :\text{y-Wert bei x=0}\to 1.03\\ {\hat{\beta }}_2& :\text{Steigung von Einkommenslinie}\\ & :\to P_1(2,1.4),P_2(1,1.2)\\ & :\to \frac{\Delta y}{\Delta x}=\frac{1.4-1.2}{2-1}=0.2\\ {\hat{\beta }}_3& :\text{vertikale Abstand zw. niedrig \& mittler}\\ & :\to \text{Bei }x=2\text{ ablesen}\\ & :\to 1.9-1.4=0.5\\ {\hat{\beta }}_4& :\text{vertikale Abstand zw. niedrig \& hoch}\\ & :\to \text{Bei }x=2\text{ ablesen}\\ & :\to 2.2-1.4=0.8\end{array}$$

Somit lauten die geschätzten Koeffizienten:

$$\begin{array}{rl}{\hat{\beta }}_0& =1.03\\ {\hat{\beta }}_2& =0.2\\ {\hat{\beta }}_3& =0.5\\ {\hat{\beta }}_4& =0.8\end{array}$$

(c) Basierend auf Modell 2.1 soll nun in einem linearen Hypothesentest der Form $A\beta =c$ die Nullhypothese überprüft werden, dass der Effekt für die Kategorie mittel im Vergleich zur Referenzkategorie doppelt so großist wie für die Kategorie hoch. Geben Sie für diesen Test die Hypothesen, die Matrizen $A$ und $c$ sowie die Verteilung der Teststatistik an.

Eugens Lösung

• Hypothesenformulierung $$\begin{array}{rl}{H}_0& :{\beta }_3-2{\beta }_4=0\\ H_A& :{\beta }_3-2{\beta }_4\ne 0\end{array}$$
• Matrizendarstellung
• Wir definieren zunächst $$\beta =\left(\begin{array}{c}{\beta }_0\\ {\beta }_1\\ {\beta }_2\\ {\beta }_3\\ {\beta }_4\end{array}\right)$$
• Matix $A$
• Wir testen auf ${\beta }_3-2{\beta }_4=0$

$$A=\left(\begin{array}{ccccc}0& 0& 0& 1& -2\end{array}\right)$$

• Hypothese in Matrixform - $A\beta =c$ wird zu

  $$\left(\begin{array}{ccccc}0& 0& 0& 1& -2\end{array}\right)\left(\begin{array}{c}{\beta }_0\\ {\beta }_1\\ {\beta }_2\\ {\beta }_3\\ {\beta }_4\end{array}\right)=(0)$$

  Die Teststatistik lautet:

$$F=(1,995)$$

1 weil wir auf eine Variable testen ${\beta }_3=2{\beta }_4$ und 995 weil wir 1000 n haben - 5 Variablen

Aufgabenstellung

Die Umfrage zum Reiseverhalten wurde auch in den folgenden vier Jahren an den gleichen Personen (id) durchgeführt. Um zu untersuchen, ob es generelle Entwicklungen bei der Reisedistanz von 2018 bis 2022 gab, wurde das folgende Random Intercept-Modell (Modell 2.2) mit der Zeit (Jahr) als zusätzlicher Kovariable gefittet.

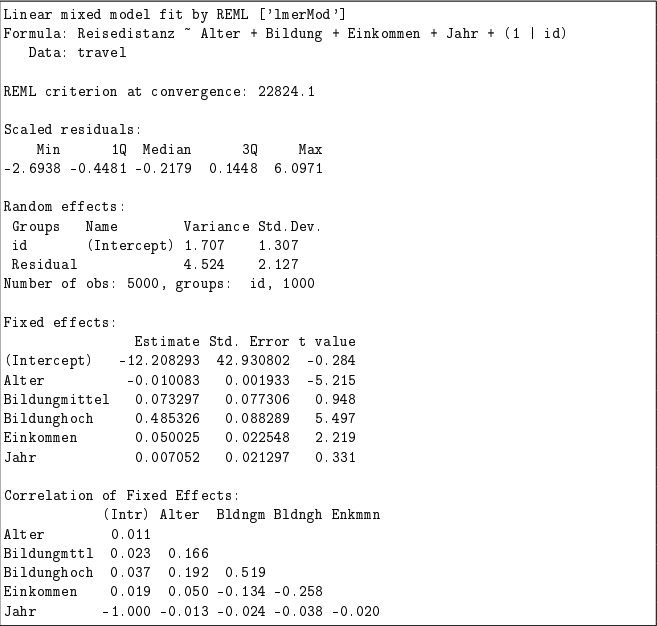
Modell 2.2

(d) Erläutern Sie zwei Gründe, warum ein Random Intercept-Modell gegenüber einem linearen Modell mit festen Effekten für die Personen bei der gegebenen Datensituation ggf. vorzuziehen ist.

Stichpunkte

• Kontrolle für unbeobachtete Heterogenität:
  • Erfasst individuelle Unterschiede, die nicht durch beobachtete Variablen erklärt werden.
  • Berücksichtigt personenspezifische Einflüsse wie persönliche Vorlieben.
• Effizientere Schätzung und Generalisierbarkeit:
  • Nutzt die Datenstruktur besser, besonders bei vielen Beobachtungen pro Person.
  • Vermeidet Reduktion der Freiheitsgrade und Überanpassung.
  • Führt zu besseren generalisierbaren Ergebnissen.

Fließtext

Ein Random Intercept-Modell kann gegenüber einem linearen Modell mit festen Effekten aus zwei Gründen vorzuziehen sein:

1. Es erfasst individuelle Unterschiede, die nicht durch beobachtete Variablen erklärt werden, und berücksichtigt personenspezifische Einflüsse wie persönliche Vorlieben.
2. Es nutzt die Datenstruktur besser, besonders bei vielen Beobachtungen pro Person, vermeidet Reduktion der Freiheitsgrade und Überanpassung und führt zu besser generalisierbaren Ergebnissen.

(e) Bestimmen und interpretieren Sie anhand des gegebenen R-Outputs zu Modell 2. 2 die Intra-Class-Correlation.

Die Intra-Class-Correlation (ICC) misst den Anteil der Gesamtvarianz eines Merkmals, der auf Unterschiede zwischen den Gruppen (oder Individuen) zurückzuführen ist, und gibt damit an, wie ähnlich die Mitglieder innerhalb einer Gruppe sind. Ein höherer ICC-Wert zeigt an, dass ein größerer Anteil der Varianz durch gruppeninterne Ähnlichkeiten erklärt wird.

$$ICC=\frac{\text{Varianz der Zufallintercepts}}{\text{Varianz der Zufallintercepts}+\text{Residumsvarianz}}$$

• ICC < 0.05:
  • Geringe Signifikanz, die meiste Varianz wird durch Fehler oder innerhalb der Gruppen erklärt.
  • Die Ähnlichkeit innerhalb der Gruppen ist sehr gering.
• 0.05 ≤ ICC < 0.10:
  • Mäßige Signifikanz.
  • Es gibt eine gewisse Ähnlichkeit innerhalb der Gruppen, aber sie ist immer noch relativ gering.
• 0.10 ≤ ICC < 0.20:
  • Mittlere Signifikanz.
  • Die Ähnlichkeit innerhalb der Gruppen ist moderat.
• 0.20 ≤ ICC < 0.30:
  • Substantielle Signifikanz.
  • Die Ähnlichkeit innerhalb der Gruppen ist beträchtlich.
• ICC ≥ 0.30:
  • Hohe Signifikanz.
  • Ein großer Teil der Varianz wird durch die Unterschiede zwischen den Gruppen erklärt.
  • Die Ähnlichkeit innerhalb der Gruppen ist hoch.

Nun einsetzen:

$$\begin{array}{rl}ICC& =\frac{1.707}{1.707+4.524}\\ & \\ & =0.27395\end{array}$$

Das bedeutet:

→ Etwa 27,4% der Varianz in der Reisedistanz zwischen den verschiedenen Personen wird durch individuelle Unterschiede erklärt. Individuelle Unterschiede zwischen Personen spielen eine Rolle

(f) Ein Forscher vermutet, dass sich der Effekt der Bildung über den betrachteten fünfjährigen Zeitraum geändert haben könnte. Erklären Sie, wie man diese Vermutung überprüfen könnte.

Stichpunkte

• Interaktionsmodell erstellen:
  • Interaktionsterm zwischen Bildung und Jahr einfügen
  • Modell: $$\text{Reisedistanz}\sim \text{Alter}+\text{Bildung}+\text{Einkommen}+\text{Jahr}+(\text{Bildung}\times \text{Jahr})+(1|\text{id})$$

Reisedistanz ~ Alter + Bildung + Einkommen + Jahr + (Bildung × Jahr) + (1 | id)

• Hypothesentest:

  • Nullhypothese: Keine Interaktion (Effekt der Bildung ändert sich nicht über die Zeit)
  • Alternativhypothese: Interaktion vorhanden (Effekt der Bildung ändert sich über die Zeit)

• Modellvergleich:

  • Vergleiche das ursprüngliche Modell mit dem Interaktionsmodell
  • Likelihood-Ratio-Test (LRT) oder Akaike-Informationskriterium (AIC)

Fließtext

Um zu überprüfen, ob sich der Effekt der Bildung über den fünfjährigen Zeitraum geändert hat, kann ein Interaktionsmodell erstellt werden, das einen Interaktionsterm zwischen Bildung und Jahr enthält:

$$\text{Reisedistanz}\sim \text{Alter}+\text{Bildung}+\text{Einkommen}+\text{Jahr}+(\text{Bildung}\times \text{Jahr})+(1|\text{id})$$

Dann wird ein Hypothesentest durchgeführt, wobei die Nullhypothese lautet, dass es keine Interaktion gibt (der Effekt der Bildung ändert sich nicht über die Zeit). Die Alternativhypothese besagt, dass eine Interaktion vorhanden ist (der Effekt der Bildung ändert sich über die Zeit).

Der Modellvergleich erfolgt mittels Likelihood-Ratio-Test (LRT) oder Akaike-Informationskriterium (AIC). Ein signifikant besseres Interaktionsmodell deutet darauf hin, dass sich der Effekt der Bildung über den Zeitraum geändert hat.

---

Aufgabe 3

Aufgabenstellung

Credit Scoring ist ein Bereich der Datenanalyse, der häufig im Bankenwesen eingesetzt wird.

Ziel ist es, anhand verschiedener personenspezifischer Merkmale (z.B. Alter) sowie Merkmale zur finanziellen Lage (z.B. Einkommen, Hauseigentum) und zur Kredithistorie (z.B. Anzahl Probleme in der Vergangenheit) auf die Kreditwürdigkeit von Bewerbern zu schließen.

Im Folgenden wird ein Datensatz zu 1319 Personen betrachtet, für die zusammen mit weiteren Variablen die Information erhoben wurde, ob ihr Antrag für eine Kreditkarte akzeptiert wurde.

Anhand des Datensatzes soll untersucht werden, auf welche Weise die verschiedenen Einflussgrößen auf die Bewilligung einer Kreditkarte durch die Bank wirken.

Im Rahmen der Aufgabe werden die folgenden Variablen betrachtet:

Variable	Beschreibung
card	Bewilligung einer Kreditkarte (0 = nein, 1 = ja)
age	Alter in Jahren
income	Jährliches Bruttoeinkommen in 10 000 USD
owner	Eigentümer eines Hauses (no = nein, yes = ja)
selfemp	Selbstständige Beschäftigung (no = nein, yes = ja)
reports	Anzahl problematischer finanzieller Interaktionen in der Vergangenheit
expenditure	Durchschnittliche monatliche Kreditkartenausgaben in USD

Zur Beantwortung der Fragestellung wird das folgende Modell (Modell 3.1) angepasst:

Modell 3.1

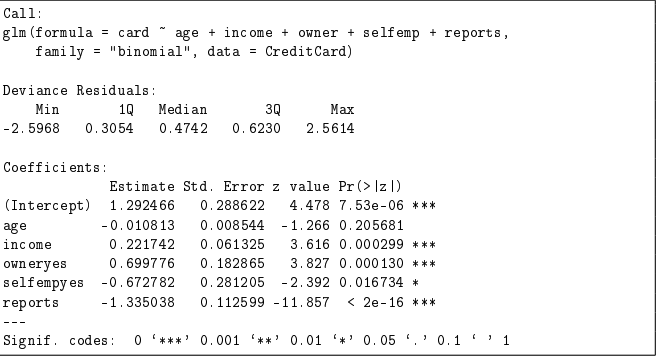
(a) Geben Sie anhand des R-Outputs zu Modell 3.1 den linearen Prädiktor, die Responsefunktion und die Verteilung der Zielvariable (gegeben die Kovariablen) an.

Eugens Lösung

• Linearer Prädiktor ($\eta$): Der lineare Prädiktor fasst die Einflüsse der Kovariablen in einem logistischen Regressionsmodell zusammen. Basierend auf dem R-Output des Modells 3.1 lautet der lineare Prädiktor:

$$\eta =1.292466+(-0.010813)\cdot \text{age}+0.221742\cdot \text{income}+0.699776\cdot \text{owner}+(-0.672782)\cdot \text{selfemp}+(-1.335038)\cdot \text{reports}$$

wobei:

• $\text{age}$ das Alter in Jahren ist,

• $\text{income}$ das jährliche Bruttoeinkommen in 10.000 USD ist,

• $\text{owner}$ ein Indikator für Hauseigentum ist (1 = ja, 0 = nein),

• $\text{selfemp}$ ein Indikator für Selbstständigkeit ist (1 = ja, 0 = nein),

• $\text{reports}$ die Anzahl problematischer finanzieller Interaktionen ist.

• Responsefunktion: Da es sich um eine logistische Regression handelt, ist die Responsefunktion die logistische Funktion (Logit-Funktion), die die Wahrscheinlichkeit berechnet, dass eine Kreditkarte bewilligt wird ($\text{card}=1$):

  $$\pi (x)=P(\text{card}=1\mid x)=\frac{1}{1+e^{-\eta }}$$

  wobei $\eta$ der lineare Prädiktor ist.

• Verteilung der Zielvariable: Die Zielvariable $\text{card}$ folgt einer binomialen Verteilung (binomial), da es sich um ein binäres Ereignis handelt (0 = Kreditkarte nicht bewilligt, 1 = Kreditkarte bewilligt).

  $$\text{card}\mid x\sim \text{Bernoulli}(\pi (x))$$

  wobei $\pi (x)$ die Wahrscheinlichkeit ist, dass eine Kreditkarte bewilligt wird, gegeben die Kovariablen $x$.

Zusammengefasst:

• Linearer Prädiktor:

  $$\eta =1.292466-0.010813\cdot \text{age}+0.221742\cdot \text{income}+0.699776\cdot \text{owner}-0.672782\cdot \text{selfemp}-1.335038\cdot \text{reports}$$

• Responsefunktion:

  $$\pi (x)=\frac{1}{1+e^{-\eta }}$$

• Verteilung der Zielvariable:

  $$\text{card}\mid x\sim \text{Bernoulli}(\pi (x))$$

(b) Interpretieren Sie die geschätzten Koeffizienten der Variablen income und owner auf Ebene der Odds.

Koeffizient für income:

• Der geschätzte Koeffizient für das Einkommen ($\text{income}$) beträgt $0.221742$.
• Interpretation: Für jede Erhöhung des jährlichen Bruttoeinkommens um 10.000 USD steigen die Odds (die Wahrscheinlichkeit, dass eine Kreditkarte bewilligt wird, im Verhältnis zur Wahrscheinlichkeit, dass sie nicht bewilligt wird) um das $e^{0.221742}$-Fache.
• Berechnung der Odds: $$e^{0.221742}\approx 1.248$$
• Das bedeutet: Bei einer Erhöhung des Einkommens um 10.000 USD erhöhen sich die Odds, eine Kreditkarte zu erhalten, um etwa 24.8 %.

Koeffizient für owner:

• Der geschätzte Koeffizient für Hauseigentum ($\text{owner}$) beträgt $0.699776$.
• Interpretation: Wenn eine Person ein Haus besitzt (owner = 1), steigen die Odds, dass eine Kreditkarte bewilligt wird, im Vergleich zu einer Person ohne Haus (owner = 0) um das $e^{0.699776}$-Fache.
• Berechnung der Odds: $$e^{0.699776}\approx 2.013$$
• Das bedeutet: Hauseigentümer haben etwa doppelt so hohe Odds (201.3 %), eine Kreditkarte bewilligt zu bekommen, verglichen mit Nicht-Hauseigentümern.

Zusammengefasst:

• income: Eine Erhöhung des Einkommens um 10.000 USD führt zu einer Erhöhung der Odds, eine Kreditkarte zu erhalten, um etwa 24.8 %.
• owner: Hauseigentümer haben etwa doppelt so hohe Odds, eine Kreditkarte bewilligt zu bekommen, verglichen mit Nicht-Hauseigentümern.

Warum nicht direkt die Wahrscheinlichkeit?

• Wahrscheinlichkeiten ändern sich nicht linear mit den Prädiktoren. Die Log-Odds ermöglichen eine lineare Beziehung, die leichter zu interpretieren ist.

Kurz: $e^{\text{Koeffizient}}$ gibt an, um wie viel sich die Odds ändern, was eine klarere Aussage über den Einfluss der Prädiktoren ermöglicht.

(c) Wie hoch ist gemäß Modell 3.1 die Chance auf die Bewilligung einer Kreditkarte für eine selbstständige Antragstellerin mit 40 000 USD Jahreseinkommen im Vergleich zu einer angestellten Antragstellerin mit 30 000 USD Jahreseinkommen, wenn alle anderen Variablen bei beiden Frauen gleich sind?

Gegebene Informationen:

• Selbstständige Antragstellerin:

  • Einkommen: 40.000 USD (income = 4)
  • selfemp = 1

• Angestellte Antragstellerin:

  • Einkommen: 30.000 USD (income = 3)
  • selfemp = 0

Koeffizienten aus Modell 3.1:

• ${\hat{\beta }}_{\text{income}}=0.221742$
• ${\hat{\beta }}_{\text{selfemp}}=-0.672782$

Berechnung der Odds:

1. Log-Odds für die selbstständige Antragstellerin:

   $${\eta }_{\text{self-employed}}=0.221742\cdot 4-0.672782=0.214186$$

2. Log-Odds für die angestellte Antragstellerin:

   $${\eta }_{\text{employed}}=0.221742\cdot 3=0.665226$$

3. Odds (Exponentialwerte der log-Odds):

   $${\text{Odds}}_{\text{self-employed}}=e^{0.214186}\approx 1.239$$ $${\text{Odds}}_{\text{employed}}=e^{0.665226}\approx 1.945$$

4. Verhältnis der Chancen:

   $$\frac{{\text{Odds}}_{\text{self-employed}}}{{\text{Odds}}_{\text{employed}}}=\frac{1.239}{1.945}\approx 0.637$$

Ergebnis:

Die Chancen auf die Bewilligung einer Kreditkarte für eine selbstständige Antragstellerin mit 40.000 USD Jahreseinkommen betragen etwa 63.7 % der Chancen einer angestellten Antragstellerin mit 30.000 USD Jahreseinkommen, wenn alle anderen Variablen gleich sind.

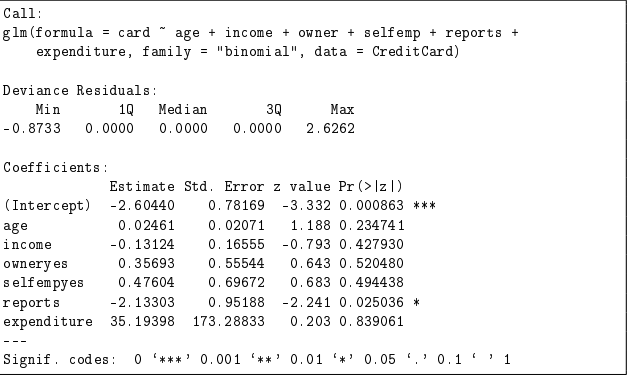
(d) Das Modell wird nun um die Variable expenditure (monatliche Kreditkartenausgaben) ergänzt, so dass sich der untenstehende Modelloutput (Modell 3.2) ergibt. Vergleichen Sie den Output mit dem Output zu Modell 3.1. Erklären Sie die Problematik, die sich bezüglich der Variable expenditure ergibt.

Modell 3.2

Eugens Lösung

Vergleich der Modelle:

Modell 3.1:

• Formel: card ~ age + income + owner + selfemp + reports
• Signifikante Variablen: income, owner, selfemp, reports

Modell 3.2:

• Formel: card ~ age + income + owner + selfemp + reports + expenditure
• Signifikante Variable: reports

Änderungen in Modell 3.2:

• Koeffizient für expenditure: sehr hoch (35.19398), aber nicht signifikant ((p = 0.839061)).
• income, owner und selfemp sind nicht mehr signifikant.

Problematik bezüglich der Variable expenditure:

1. Multikollinearität:

• Die Variable expenditure könnte stark mit anderen Variablen korreliert sein, insbesondere mit income und reports. Dies führt zu Multikollinearität, die die Schätzungen der Koeffizienten instabil und unzuverlässig macht.

2. Überanpassung:

• Der sehr hohe Koeffizient für expenditure deutet darauf hin, dass diese Variable möglicherweise zu Überanpassung führt. Dies bedeutet, dass das Modell sehr gut auf die Trainingsdaten passt, aber möglicherweise schlechter auf neue Daten generalisiert.

3. Interpretation:

• Die mangelnde Signifikanz der Variable expenditure trotz des hohen Koeffizienten und der hohen Standardabweichung (173.28833) deutet darauf hin, dass diese Variable wenig zur Erklärung der Kreditkartenbewilligung beiträgt und möglicherweise Rauschen (Zufallseffekte) im Modell einführt.

Zusammengefasst

Zusammengefasst hat die Aufnahme der Variable expenditure in Modell 3.2 die Signifikanz der anderen Variablen beeinflusst und könnte auf Probleme wie Multikollinearität und Überanpassung hinweisen.

(e) Die folgende Tabelle gibt für einen Validierungsdatensatz mit fünf Antragstellern die anhand von Modell 3.1 prognostizierten Wahrscheinlichkeiten für eine Bewilligung einer Kreditkarte an.

Antragsteller	1	2	3	4	5
P(card = 1|x)	0.96	0.89	0.61	0.53	0.07
card	Ja	Ja	Nein	Ja	Nein

(i) Zeichnen Sie die ROC-Kurve für diesen Datensatz. Geben Sie die hierfür berechneten Punkte im Koordinatensystem an.

Berechnung der ROC-Kurve

Um die ROC-Kurve zu berechnen, folgen Sie diesen Schritten:

1. Sortieren: Sortieren Sie die prognostizierten Wahrscheinlichkeiten $P(\text{card}=1|x)$ der Antragsteller in absteigender Reihenfolge.

2. Schwellenwerte festlegen: Verwenden Sie die sortierten Wahrscheinlichkeiten als Schwellenwerte.

3. Berechnen: Für jede Schwelle:

   • True Positives (TP): Anzahl der korrekt als “Ja” klassifizierten Fälle.
   • False Positives (FP): Anzahl der fälschlicherweise als “Ja” klassifizierten Fälle.
   • True Negatives (TN): Anzahl der korrekt als “Nein” klassifizierten Fälle.
   • False Negatives (FN): Anzahl der fälschlicherweise als “Nein” klassifizierten Fälle.

   Berechnen Sie die Raten:

   • True Positive Rate (TPR): $\text{TPR}=\frac{TP}{TP+FN}$
   • False Positive Rate (FPR): $\text{FPR}=\frac{FP}{FP+TN}$

4. Punkte plotten: Plotten Sie die TPR gegen die FPR für jede Schwelle.

Die ROC-Kurve ist die grafische Darstellung der TPR gegen die FPR bei verschiedenen Schwellenwerten.

---

Berechnung

• Bei Schwellenwert $\ge 0.96$:
  • TPR = $\frac{1}{3}=0.33$ (1 von 3 positiven Fällen erkannt)
  • FPR = $\frac{0}{2}=0.0$ (0 von 2 negativen Fällen fälschlicherweise erkannt)
• Bei Schwellenwert $\ge 0.89$:
  • TPR = $\frac{2}{3}=0.67$ (2 von 3 positiven Fällen erkannt)
  • FPR = $\frac{0}{2}=0.0$ (0 von 2 negativen Fällen fälschlicherweise erkannt)
• Bei Schwellenwert $\ge 0.61$:
  • TPR = $\frac{2}{3}=0.67$ (2 von 3 positiven Fällen erkannt)
  • FPR = $\frac{1}{2}=0.5$ (1 von 2 negativen Fällen fälschlicherweise erkannt)
• Bei Schwellenwert $\ge 0.53$:
  • TPR = $\frac{3}{3}=1.00$ (3 von 3 positiven Fällen erkannt)
  • FPR = $\frac{1}{2}=0.5$ (1 von 2 negativen Fällen fälschlicherweise erkannt)
• Bei Schwellenwert $\ge 0.07$:
  • TPR = $\frac{3}{3}=1.00$ (3 von 3 positiven Fällen erkannt)
  • FPR = $\frac{2}{2}=1.0$ (2 von 2 negativen Fällen fälschlicherweise erkannt)

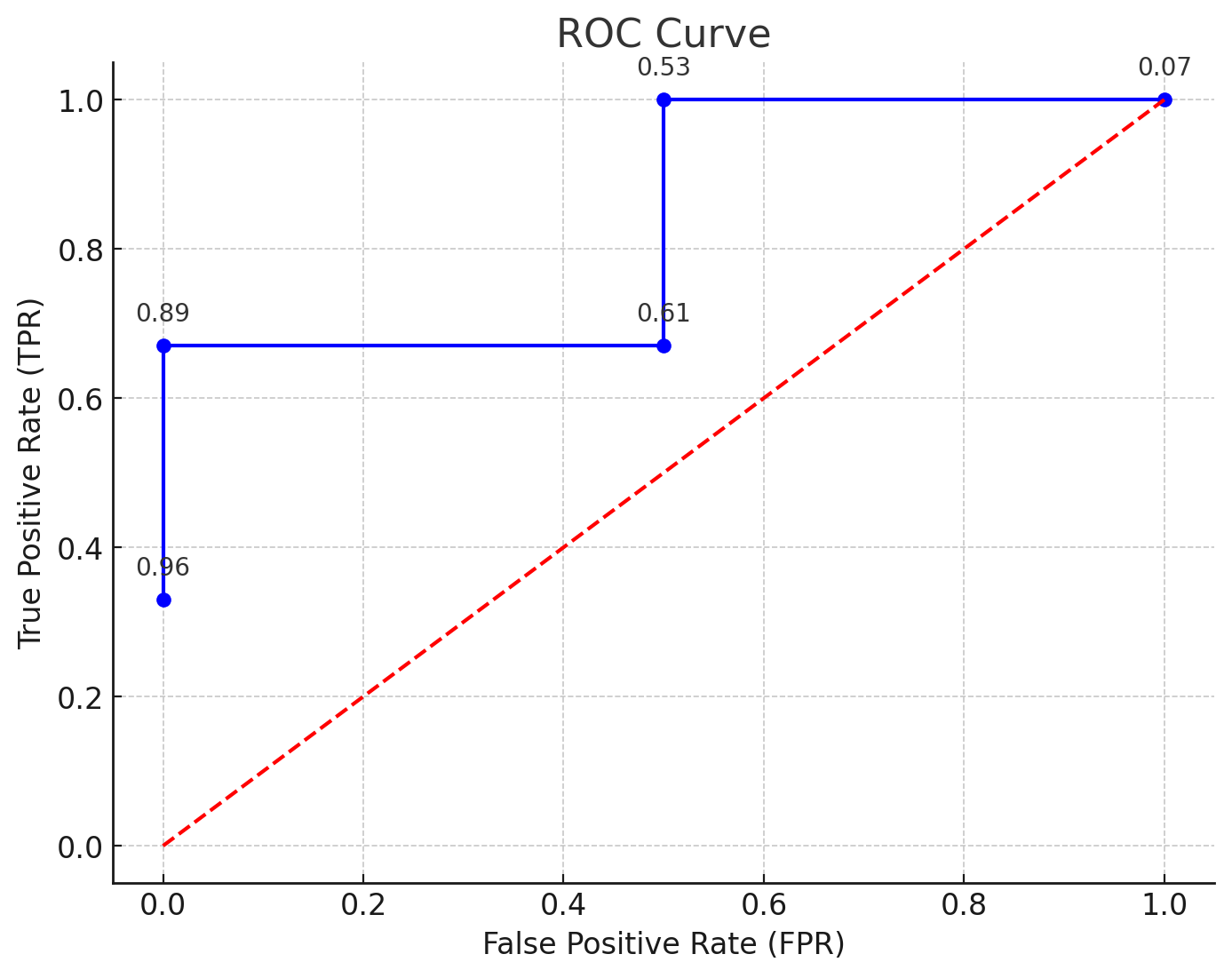
(ii) Berechnen Sie den AUC-Wert.

• Links oben haben wir ein schönes Rechteck mit dem wir die AUC berechnen können

$$1-\frac{1}{3}\cdot 0.5=0.8333$$

oder

$$\text{AUC}=\frac{2}{3}\cdot \frac{1}{2}+1\cdot \frac{1}{2}=\frac{5}{6}=0.8\overline{3}$$

• 1/3 * 0.5 berechnet Flächeninhalt blaues viereck links oben
• 1-Fläche dieser kehrt diese um und gibt uns die AUC

---

Aufgabe 4 (irrelevant für Info)

Aufgabenstellung

Im Rahmen dieser Aufgabe soll die Mortalität (pro 100 000 Einwohner) in Metropolregionen in den USA in Abhängigkeit von bis zu 15 Kovariablen modelliert werden. Hierfür wird ein Datensatz verwendet, der 1973 von McDonald und Schwing veröffentlicht wurde.

(a) Zunächst wird ein lineares Modell geschätzt, bei dem alle 15 möglichen Einflussgrößen berücksichtigt werden. Interpretieren Sie das $R^2$ anhand des folgenden gekürzten R-Outputs.

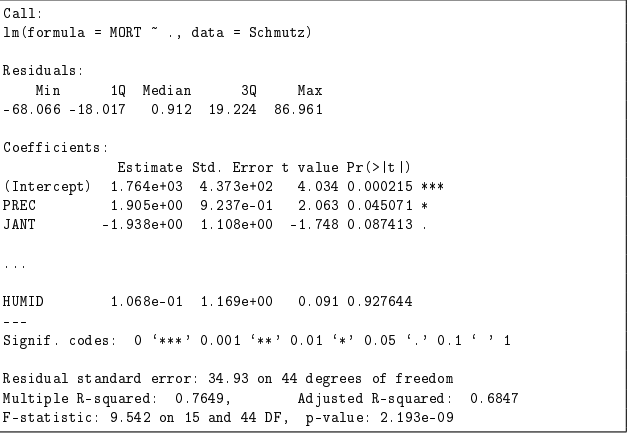
Stichpunkte:

• Multiple R-squared: 0.7649
  • Bedeutet, dass 76.49% der Varianz der Mortalität durch das Modell erklärt werden.
• Adjusted R-squared: 0.6847
  • Berücksichtigt die Anzahl der Prädiktoren und zeigt, dass 68.47% der Varianz erklärt werden.
• Fazit: Gute Modellanpassung.

Fließtext:

Der Multiple R-squared-Wert von 0.7649 bedeutet, dass 76.49% der Varianz der Mortalität durch das Modell erklärt werden. Der Adjusted R-squared-Wert von 0.6847 berücksichtigt die Anzahl der Prädiktoren und zeigt, dass das Modell immer noch 68.47% der Varianz erklärt. Insgesamt deutet dies auf eine gute Modellanpassung hin.

(b) Der folgende R-Code führt vier verschiedene schrittweise Variablenselektionsverfahren zur Modellierung der Mortalität durch. Die Ergebnisse werden in den Objekten Selektion_1, Selektion_2, Selektion_3 und Selektion_4 gespeichert.

Volles_Modell <- lm(MORT ~ ., data = SCHMUTZ)
Null_Modell <- lm(MORT ~ 1, data = Schmutz)
scope_schmutz <- list(upper = Volles_Modell, lower = Null_Modell)
Selektion_1 <- stepAIC(Null_Modell, scope = scope_schmutz,
                        direction = "forward", k = log(nrow(Schmutz)))
Selektion_2 <- stepAIC(Volles_Modell, scope = scope_schmutz,
                        direction = "backward")
Selektion_3 <- stepAIC(Null_Modell, scope = scope_schmutz,
                        direction = "both")
Selektion_4 <- stepAIC(Volles_Modell, scope = scope_schmutz,
                        direction = "both", k = log(nrow(Schmutz)))

(i) Bestimmen Sie für jedes der vier Variablenselektionsverfahren, welches Selektionskriterium und welche Selektionsmethode verwendet wurden. Geben Sie auch jeweils an, ob das Verfahren mit dem Nullmodell oder dem vollen Modell gestartet wurde.

Eugens Lösung

Erklärung: Selektionskriterium,-methode, Null/-Volles-Modell

Erklärungen in ausführlicheren Stichpunkten:

• Selektionskriterium:
  • Bewertet die Güte eines Regressionsmodells.
  • Beispiele:
    • Akaike-Informationskriterium (AIC): Bestraft Modellkomplexität, um Überanpassung zu vermeiden.
    • Bayesianisches Informationskriterium (BIC): Ähnlich wie AIC, aber mit stärkerer Bestrafung für Modellkomplexität.
  • Ziel: Balance zwischen Anpassungsgüte (wie gut das Modell die Daten erklärt) und Komplexität (Anzahl der Variablen).
• Selektionsmethode:
  • Vorgehensweise zur Auswahl der besten Variablenkombination für ein Modell.
  • Vorwärtsselektion:
    • Startet mit einem Nullmodell (nur Achsenabschnitt).
    • Fügt schrittweise die Variablen hinzu, die die Modellgüte am meisten verbessern.
  • Rückwärtsselektion:
    • Startet mit einem vollen Modell (alle Variablen enthalten).
    • Entfernt schrittweise die Variablen, die die Modellgüte am wenigsten beeinträchtigen.
  • Stepwise-Selektion:
    • Kombiniert Vorwärts- und Rückwärtsselektion.
    • Variablen werden hinzugefügt oder entfernt, um das beste Modell zu finden.
• Nullmodell:
  • Einfachstes Modell, enthält keine erklärenden Variablen.
  • Nur der Achsenabschnitt (Intercept) ist im Modell.
  • Dient als Ausgangspunkt für Vorwärtsselektion oder Stepwise-Selektion, die mit einem leeren Modell beginnen.
• Volles Modell:
  • Komplexestes Modell, enthält alle verfügbaren erklärenden Variablen.
  • Dient als Ausgangspunkt für Rückwärtsselektion oder Stepwise-Selektion, die mit einem Modell beginnen, das alle Variablen enthält.

1. Selektion_1

   • Selektionskriterium: Akaike-Informationskriterium (BIC) mit Anpassung für große Stichproben ($k=\log (n)$).
   • Selektionsmethode: Vorwärtsselektion.
   • Startmodell: Nullmodell.

2. Selektion_2

   • Selektionskriterium: Akaike-Informationskriterium (AIC).
   • Selektionsmethode: Rückwärtsselektion.
   • Startmodell: Volles Modell.

3. Selektion_3

   • Selektionskriterium: Akaike-Informationskriterium (AIC).
   • Selektionsmethode: Beide Richtungen (Stepwise).
   • Startmodell: Nullmodell.

4. Selektion_4

   • Selektionskriterium: Akaike-Informationskriterium (AIC) mit Anpassung für große Stichproben ($k=\log (n)$).
   • Selektionsmethode: Beide Richtungen (Stepwise).
   • Startmodell: Volles Modell.

(ii) Begründen Sie, ohne die Ergebnisse der Variablenselektion zu kennen, welches der vier Verfahren wahrscheinlich zum kleinsten Modell führen wird.

Das Verfahren, das wahrscheinlich zum kleinsten Modell führen wird, ist Selektion_1.

Begründung:

• Selektion_1 verwendet Vorwärtsselektion, die mit dem Nullmodell startet und schrittweise Variablen hinzufügt, nur wenn diese eine signifikante Verbesserung des Modells bewirken.
• Das Selektionskriterium $k=\log (n)$ ist strenger als das standardmäßige AIC, da es eine größere Strafe für zusätzliche Variablen beinhaltet. Dies führt tendenziell zu Modellen mit weniger Variablen, da nur Variablen, die eine substanzielle Verbesserung des Modells liefern, aufgenommen werden.
• Im Vergleich zu Rückwärtsselektion (Selektion_2) und Stepwise-Verfahren (Selektion_3 und Selektion_4), die mit dem vollen Modell starten oder weniger strenge Kriterien verwenden, wird Vorwärtsselektion mit einem strengen Kriterium am ehesten ein sparsames Modell produzieren.

(iii) Verwenden Sie den folgenden R-Code, um zu begründen, welches der vier Variablenselektionsverfahren zur Prognose neuer Datenpunkte ausgewählt werden würden.

####### Dimensionen der neuen Daten #######
dim(Neu_Daten)
# 100 Reihen, 16 Spalten
 
####### Funktion zur Berechnung des Root Mean Squared Error #######
RMSE <- function(Y, Y_pred){
  RMSE <- sqrt(sum((Y - Y_pred)^2))
  return(RMSE)
}
 
####### Prognose der Mortalität anhand der vier #######
####### Variablenselektionsverfahren für die neuen Daten #######
Predict_1 <- predict(Selektion_1, newdata = Neu_Daten)
Predict_2 <- predict(Selektion_2, newdata = Neu_Daten)
Predict_3 <- predict(Selektion_3, newdata = Neu_Daten)
Predict_4 <- predict(Selektion_4, newdata = Neu_Daten)
 
####### Auflistung der berechneten RMSEs #######
RMSE_SELEKTION <- cbind("Selektion_1"= RMSE(Neu_Daten$MORT, Predict_1),
                        "Selektion_2"= RMSE(Neu_Daten$MORT, Predict_2),
                        "Selektion_3"= RMSE(Neu_Daten$MORT, Predict_3),
                        "Selektion_4"= RMSE(Neu_Daten$MORT, Predict_4))
 
 
RMSE_SELEKTION
|      | Selektion_1 | Selektion_2 | Selektion_3 | Selektion_4 |
| ---- | ----------- | ----------- | ----------- | ----------- |
| RMSE | 231.6872    | 431.1707    | 231.6872    | 431.1707    |
 

• Analyse: Der RMSE-Wert misst die durchschnittliche Abweichung zwischen den vorhergesagten und den tatsächlichen Werten. Ein niedrigerer RMSE-Wert zeigt eine bessere Vorhersagegenauigkeit.

• Ergebnis: Die Verfahren Selektion_1 und Selektion_3 haben die niedrigsten RMSE-Werte (231.6872), was bedeutet, dass sie die besten Vorhersagegenauigkeiten aufweisen.

• Begründung: Basierend auf den RMSE-Werten würde Selektion_1 oder Selektion_3 zur Prognose neuer Datenpunkte ausgewählt werden, da sie die geringste Abweichung und somit die beste Vorhersagegenauigkeit bieten.

Erklärung: RMSE (Root Mean Squared Error)

Erklärungen in ausführlicheren Stichpunkten:

• RMSE:
  • Steht für Root Mean Squared Error.
  • Bewertet die durchschnittliche Abweichung zwischen den vorhergesagten und den tatsächlichen Werten.
  • Berechnung: Wurzel des Durchschnitts der quadrierten Differenzen zwischen den vorhergesagten und den tatsächlichen Werten.
• Funktion:
  • Misst die Genauigkeit eines Vorhersagemodells.
  • Ein niedrigerer RMSE-Wert zeigt eine höhere Vorhersagegenauigkeit.
• Anwendung:
  • Verwendet, um die Leistung verschiedener Modelle zu vergleichen.
  • Hilft bei der Auswahl des Modells, das die besten Vorhersagen für neue Datenpunkte liefert.

(iv) Geben sie einen Grund an, warum sich für zwei verschiedene Variablenselektionsverfahren die gleichen RMSEs ergeben können.

Zwei verschiedene Variablenselektionsverfahren können gleiche RMSEs ergeben, wenn sie die gleichen Variablen im endgültigen Modell haben. Dies kann passieren, wenn:

• Gleiche Schlüsselvariablen: Beide Verfahren identifizieren und behalten die gleichen wichtigsten Variablen im Modell.
• Redundante Variablen: Wenn viele Variablen stark korreliert sind, können verschiedene Verfahren ähnliche Variablenkombinationen auswählen, die dieselbe Vorhersagekraft haben.
• Ähnliche Modellkomplexität: Beide Modelle können trotz unterschiedlicher Ansätze zur gleichen Anzahl an Variablen im Endmodell führen.

(c) Beschreiben Sie je einen möglichen Vor- und Nachteil einer schrittweisen Variablenselektion gegenüber der Best Subset-Methode.

• Vorteile der schrittweisen Variablenselektion:

  • Rechenaufwand: Weniger rechenintensiv und schneller als die Best Subset-Methode, besonders bei Datensätzen mit vielen Variablen.
  • Praktische Anwendbarkeit: Einfacher in der Anwendung, da sie schrittweise Variablen hinzufügt oder entfernt, ohne alle möglichen Modelle durchprobieren zu müssen.
  • Flexibilität: Ermöglicht die Nutzung verschiedener Selektionskriterien und Methoden (vorwärts, rückwärts, beides), die auf spezifische Modellanforderungen zugeschnitten werden können.

• Nachteile der schrittweisen Variablenselektion:

  • Suboptimale Modelle: Kann in lokale Optima geraten und möglicherweise nicht das global beste Modell finden, da nicht alle Variablenkombinationen geprüft werden.
  • Überanpassung: Bei zu vielen Iterationen besteht das Risiko, dass das Modell zu stark an die Trainingsdaten angepasst wird und die Generalisierungsfähigkeit leidet.
  • Instabilität: Die Auswahl der Variablen kann instabil sein und stark variieren, wenn sich die Daten geringfügig ändern, was zu unterschiedlichen Modellen führen kann.

Erklärung: Best-Subset-Methode

• Best-Subset-Methode:
  • Ansatz: Prüft alle möglichen Kombinationen von Variablen, um das beste Modell zu finden.
  • Vorgehensweise:
    • Für einen Datensatz mit ( p ) Variablen werden alle ( 2^p ) möglichen Modelle erstellt und verglichen.
    • Jedes Modell wird anhand eines Selektionskriteriums bewertet (z.B. AIC, BIC, R-squared).
    • Das Modell mit der besten Bewertung wird ausgewählt.
  • Vorteil: Findet garantiert das Modell mit der besten Anpassung, da alle Kombinationen geprüft werden.
  • Nachteil: Sehr rechenintensiv und zeitaufwendig, besonders bei großen Datensätzen mit vielen Variablen.

(d) Stellen Sie sich nun vor, dass ein schrittweises Variablenselektionsverfahren mit dem $R^2$ als Selektionskriterium durchgeführt wird. Begründen Sie, wie viele Variablen durch dieses Selektionsverfahren ausgewählt werden würden.

Eugens Lösung

• Selektionskriterium $R^2$:

  • $R^2$ misst den Anteil der Varianz der abhängigen Variable, der durch das Modell erklärt wird.
  • Höherer $R^2$-Wert bedeutet besseres Modell.

• Schrittweise Variablenselektion:

  • Das Verfahren fügt Variablen hinzu, solange sie den $R^2$-Wert verbessern.

• Eigenschaft von $R^2$:

  • $R^2$ steigt mit jeder zusätzlichen Variable, unabhängig von deren tatsächlicher Relevanz.
  • Kann zur Überanpassung führen, wenn zu viele Variablen aufgenommen werden.

• Anzahl der Variablen:

  • Theoretisch würde das Verfahren alle verfügbaren Variablen aufnehmen, weil jede zusätzliche Variable den $R^2$-Wert erhöht.
  • Praktisch könnten jedoch andere Kriterien (z.B. p-Werte oder Adjusted $R^2$) oder eine Stop-Bedingung verwendet werden, um das Modell zu regulieren.

• Fazit:

  • Ohne zusätzliche Beschränkungen würde ein schrittweises Selektionsverfahren mit $R^2$ als Kriterium alle Variablen auswählen, um den $R^2$-Wert zu maximieren.
  • Dies würde zu einem Modell mit maximaler Komplexität führen, was jedoch nicht immer optimal ist.

---

Aufgabe 5

Aufgabenstellung

Die folgenden Aufgabenstellungen stellen offene Fragen dar, die in Textform beantwortet werden sollen. Achten Sie dabei insbesondere darauf, dass Sie Ihre eigenen Worte verwenden.

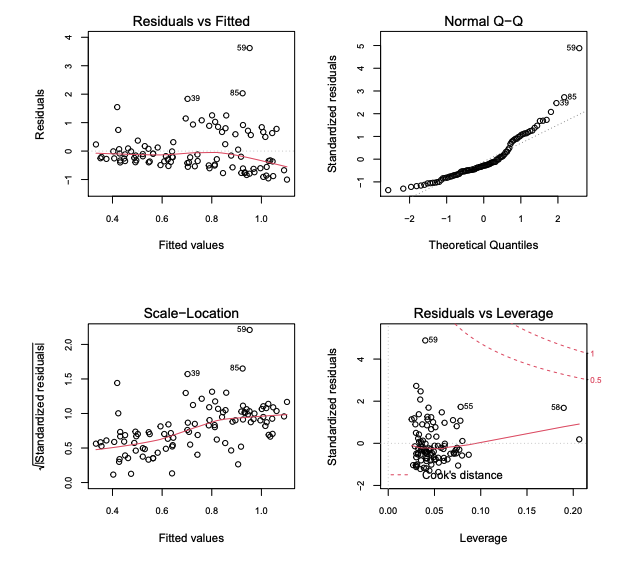
(a) Im Folgenden sind vier Standarddiagnostikgrafiken zu einem linearen Regressionsmodell der Form $y=X\beta +ϵ$ mit $ϵ\sim N(0,{\sigma }^{2}I)$ gegeben. Beurteilen Sie die Varianzhomogenitäts- und Normalverteilungsannahme des Modells und gehen Sie außerdem darauf ein, ob Ausreißer und einflussreiche Beobachtungen vorliegen. Begründen Sie Ihre Aussagen anhand der passenden Grafiken.

Spickzettel: Beurteilung von Diagnostikgrafiken für lineare Regressionsmodelle

Schritte zur Beurteilung:

1. Residuals vs. Fitted Plot:
   • Zweck: Überprüfen der Varianzhomogenität (Homoskedastizität).
   • Interpretation:
     • Gleichmäßige Verteilung der Residuen ohne Muster → Homoskedastizität.
     • Trichterförmiges Muster → Heteroskedastizität.
   • Schritte:
     • Schaue auf die Verteilung der Punkte.
     • Achte auf auffällige Muster oder Ausreißer.
2. Normal Q-Q Plot:
   • Zweck: Überprüfen der Normalverteilung der Residuen.
   • Interpretation:
     • Punkte auf der Linie → Normalverteilung.
     • Punkte weichen stark ab → Nicht-Normalverteilung.
   • Schritte:
     • Vergleiche die Punkte mit der diagonalen Linie.
     • Beachte Abweichungen an den Enden der Verteilung.
3. Scale-Location Plot:
   • Zweck: Weitere Überprüfung der Varianzhomogenität.
   • Interpretation:
     • Zufällige Verteilung der Punkte → Homoskedastizität.
     • Systematische Muster → Heteroskedastizität.
   • Schritte:
     • Schaue auf die Verteilung der Punkte.
     • Achte auf systematische Muster oder Abweichungen.
4. Residuals vs. Leverage Plot:
   • Zweck: Identifizieren einflussreicher Beobachtungen.
   • Interpretation:
     • Hohe Residuen und Hebelwirkung → potenziell einflussreiche Punkte.
   • Schritte:
     • Suche nach Punkten mit hoher Hebelwirkung und großen Residuen.
     • Beachte Punkte mit Cook’s Distance > 1.

Zusammenfassung:

• Varianzhomogenität: Prüfen auf konstante Varianz in Residuals vs. Fitted und Scale-Location Plots.
• Normalverteilung: Prüfen im Normal Q-Q Plot.
• Ausreißer und einflussreiche Beobachtungen: Identifizieren im Residuals vs. Leverage Plot.

Eugens Lösung

1. Residuals vs. Fitted Plot:

   • Varianzhomogenität: Kein eindeutiges Muster, aber einige Punkte (z.B. 39, 85) deuten auf mögliche Heteroskedastizität hin.

2. Normal Q-Q Plot:

   • Normalverteilung: Die meisten Punkte liegen entlang der Linie, jedoch Abweichungen an den Enden, insbesondere Punkt 59, was auf Nicht-Normalität hinweist.

3. Scale-Location Plot:

   • Varianzhomogenität: Einige Punkte (z.B. 39, 85,59) zeigen größere Abweichungen, was auf Probleme mit der Homoskedastizität hinweist.

4. Residuals vs. Leverage Plot:

   • Einflussreiche Beobachtungen: Punkte wie 580 und 59 haben hohe Residuen und Hebelwirkung, sind potenziell einflussreich.

Zusammenfassung:

• Hinweise auf Varianzprobleme und Nicht-Normalität der Residuen.
• Einflussreiche Beobachtungen (z.B. 85, 59) könnten das Modell stark beeinflussen und sollten weiter untersucht werden.

(b) Beschreiben Sie die Problematik der Kollinearität bei einem multiplen linearen Regressionsmodell. Warum ist es wichtig, das Modell diesbezüglich zu überprüfen und ggf. Anpassungen vorzunehmen?

Eugens Lösung

• Kollinearität:

  • Definition: Starke Korrelation zwischen zwei oder mehr unabhängigen Variablen.
  • Problem: Instabile Schätzungen der Regressionskoeffizienten.

• Wichtigkeit der Überprüfung:

  • Instabile Koeffizienten: Kleine Datenänderungen führen zu großen Schwankungen.
  • Schwierige Interpretation: Unklar, welche Variable welchen Einfluss hat.
  • Reduzierte Modellgüte: Beeinträchtigung der Modellleistung und Vorhersagekraft.

• Maßnahmen:

  • Variablenselektion: Entfernen stark korrelierter Variablen.
  • PCA: Hauptkomponentenanalyse zur Transformation in unkorrelierte Komponenten.
  • Regularisierung: Nutzung von Ridge- oder Lasso-Regression.

Zusammenfassung:

Kollinearität verursacht instabile Schätzungen und Interpretationsprobleme. Daher ist es wichtig, sie zu überprüfen und Anpassungen vorzunehmen, um die Stabilität und Vorhersagekraft des Modells zu verbessern.

(c) Erläutern Sie den Unterschied zwischen einem Konfidenz- und einem Prognoseintervall für die Prognose ${\hat{y}}_{n+1}$ einer neuen Beobachtung anhand eines linearen Modells der Form $y=X\beta +ϵ$ mit $ϵ\sim N(0,{\sigma }^{2}I)$. Welches der beiden Intervalle ist breiter?

• Konfidenzintervall:

  • Definition: Bereich, der den wahren Mittelwert der Zielvariablen für gegebene Prädiktorwerte mit einer bestimmten Wahrscheinlichkeit einschließt.
  • Zweck: Schätzung des Mittelwerts der Zielvariablen für neue Beobachtungen.
  • Breite: Schmaler als das Prognoseintervall, da nur die Unsicherheit um den geschätzten Mittelwert berücksichtigt wird.

• Prognoseintervall:

  • Definition: Bereich, der einen zukünftigen einzelnen Beobachtungswert der Zielvariablen mit einer bestimmten Wahrscheinlichkeit einschließt.
  • Zweck: Vorhersage eines einzelnen zukünftigen Werts der Zielvariablen.
  • Breite: Breiter als das Konfidenzintervall, da es sowohl die Unsicherheit um den geschätzten Mittelwert als auch die Streuung der zukünftigen Beobachtungen berücksichtigt.

Vergleich und Breite der Intervalle

• Breiteres Intervall: Das Prognoseintervall ist breiter als das Konfidenzintervall, weil es die zusätzliche Unsicherheit der individuellen Beobachtungen miteinbezieht.

Zusammenfassung

Das Konfidenzintervall schätzt den Mittelwert für neue Beobachtungen, während das Prognoseintervall einen Bereich für einzelne zukünftige Beobachtungen angibt. Aufgrund der zusätzlichen Unsicherheit ist das Prognoseintervall breiter.

(d) Erklären Sie, in welchen Datensituationen die Anwendung eines gemischten linearen Modells sinnvoll sein kann. Welche Annahme des multiplen linearen Modells wird bei einem gemischten linearen Modell aufgehoben?

Spickzettel: Gemischtes lineares Modell vs. Multiples lineares Modell

Multiples lineares Modell

• Definition: Modelliert die Beziehung zwischen einer abhängigen Variable und mehreren unabhängigen Variablen.
• Formel: $y=X\beta +ϵ$
  • $y$: Abhängige Variable
  • $X$: Matrix der unabhängigen Variablen
  • $\beta$: Vektor der Regressionskoeffizienten
  • $ϵ$: Fehlerterm, angenommen $ϵ\sim N(0,{\sigma }^{2}I)$
• Annahmen:
  • Lineare Beziehung zwischen den Variablen
  • Unabhängige und identisch verteilte Fehlerterme (Homoskedastizität)
  • Keine perfekte Multikollinearität
  • Unabhängigkeit der Beobachtungen
• Verwendung: Bei einfachen Datensätzen ohne hierarchische Struktur oder wiederholte Messungen.

Gemischtes lineares Modell

• Definition: Erweiterung des multiplen linearen Modells, das sowohl feste als auch zufällige Effekte berücksichtigt.
• Formel: $y=X\beta +Z\gamma +ϵ$
  • $y$: Abhängige Variable
  • $X$: Matrix der festen Effekte
  • $\beta$: Vektor der festen Effekte
  • $Z$: Matrix der zufälligen Effekte
  • $\gamma$: Vektor der zufälligen Effekte
  • $ϵ$: Fehlerterm
• Annahmen:
  • Lineare Beziehung zwischen den festen Effekten und der abhängigen Variable
  • Modelliert Abhängigkeiten innerhalb von Gruppen durch zufällige Effekte
  • Erlaubt Korrelationen und heterogene Varianzstrukturen
• Verwendung: Bei hierarchischen Daten, längsschnittlichen Daten oder Daten mit Gruppierungseffekten, wo die Annahme der Unabhängigkeit der Beobachtungen verletzt ist.
• Vorteil: Flexibilität in der Modellierung von komplexen Datenstrukturen und Berücksichtigung der Abhängigkeiten innerhalb von Gruppen.

• Datensituationen für gemischte lineare Modelle:

  • Hierarchische Daten: Daten, die eine verschachtelte Struktur haben, wie z.B. Schüler innerhalb von Klassen, Patienten innerhalb von Krankenhäusern.
  • Längsschnittdaten: Daten, die wiederholte Messungen derselben Individuen über die Zeit enthalten.
  • Gruppierungseffekte: Daten, bei denen Beobachtungen innerhalb von Gruppen ähnlicher sind als zwischen Gruppen.

• Aufgehobene Annahme des multiplen linearen Modells:

  • Unabhängigkeit der Beobachtungen: In multiplen linearen Modellen wird angenommen, dass die Beobachtungen unabhängig voneinander sind. Diese Annahme wird bei gemischten linearen Modellen aufgehoben, um die Korrelationen innerhalb von Gruppen oder die Abhängigkeit der Daten zu berücksichtigen.

Zusammenfassung

Gemischte lineare Modelle sind sinnvoll bei hierarchischen, längsschnittlichen oder gruppierten Daten, wo die Annahme der Unabhängigkeit der Beobachtungen verletzt ist. Sie erlauben die Modellierung von Korrelationen und Abhängigkeiten innerhalb der Datenstruktur.

(e) Erklären Sie, warum die logistische Regression im Gegensatz zur linearen Regression eine geeignete Methode für die Vorhersage von Wahrscheinlichkeiten darstellt.

Eugens Lösung

• Vorhersagebereich:

  • Lineare Regression: Kann Werte außerhalb von 0 und 1 vorhersagen, was für Wahrscheinlichkeiten ungeeignet ist.
  • Logistische Regression: Beschränkt Vorhersagen auf 0 bis 1.

• Modellierung:

  • Logistische Regression: Modelliert die Log-Odds (Logit) der Wahrscheinlichkeit.
  • Formel: $\text{logit}(p)=\log \left(\frac{p}{1-p}\right)=X\beta$

• S-förmige Kurve:

  • Sigmoid-Funktion: Beschränkt den Wertebereich auf 0 bis 1 und bietet eine glatte Übergangsfläche.

• Interpretierbarkeit:

  • Wahrscheinlichkeiten: Liefert direkt Wahrscheinlichkeiten, was die Interpretation erleichtert.

Zusammenfassung

Die logistische Regression ist besser für die Vorhersage von Wahrscheinlichkeiten geeignet, da sie Vorhersagen auf den Bereich 0 bis 1 beschränkt und eine sinnvolle Interpretation von Wahrscheinlichkeiten ermöglicht, im Gegensatz zur linearen Regression.

---